- ПОДОБНАЯ СТАТИСТИКА
- статистика, имеющая одно и то же распределение вероятностей при справедливости нек-рой сложной гипотезы.
Пусть статистика Тотображает выборочное пространство
, в измеримое пространство 
и пусть рассматривается нек-рая сложная гипотеза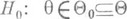 
. В таком случае, если для любого события 
вероятность Pq(T-1(B)). не зависит от q, когда 
, (*) то говорят, что Тявляется П. с. по отношению к гипотезе Н 0 или просто П. <с. Очевидно, что условие (*) равносильно тому, что распределение статистики Тне меняется, когда q пробегает Q0. Имея в виду это свойство, часто о П. с. говорят, что она является свободной относительно параметра 
. П. с. играют большую роль при построении подобных критериев, а также при решении статистич. задач с мешающими параметрами.
Пример1. Пусть X1, Х 2 ,. . ., Х п- независимые одинаково нормально N1(a,s2) распределенные случайные величины
. Тогда при любом a>0 статистика
где
является свободной относительно двумерного параметра (а, s2).
Пример 2. Пусть X1, Х 2, . . ., Х п+т - независимые одинаково распределенные случайные величины, функция распределения к-рых принадлежит семейству
всех непрерывных функций распределений на 
. В этом случае, если Fn(x).и Fm(x).суть функции эмпирич. распределений, построенные по наблюдениям X1, Х 2, . . ., X п и Х п+1, Х п+2,. . ., Х п+т соответственно, то статистика Смирнова
является подобной относительно семейства
.
Лит.:[1] Соле Ж. - Л., Основные структуры математической статистики, пер. с франц., М., 1972; [2] Липник Ю. В., Статистические задачи с мешающими параметрами, М., 1966; [3] Барра Ж. - Р., Основные понятия математической статистики, пер. с франц., М., 1974. М. С. Никулин.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
