ПЕРЕДАТОЧНАЯ ФУНКЦИЯ

линейной стационарной системы управления (системы автоматич. регулирования) - Лапласа преобразование отклика системы на воздействие единичной импульсной функции (дельта-функции) 6 (г) при нулевых условиях в момент t=0 (сам этот отклик наз. функцией веса, импульсной переходной функцией или импульсной характеристикой системы). Эквивалентное определение: П. ф. есть отношение изображений по Лапласу (см. Операционное исчисление).выходного и входного сигналов с нулевыми начальными данными. П. ф. представляет собой дробно-рациональную функцию W(p).комплексного переменного р;она является коэффициентом в линейном соотношении

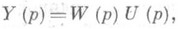(1)

связывающем изображение по Лапласу U(р).входа системы (воздействия, управления) и(t).и изображение по Лапласу Y(р).выхода системы (отклика, реакции) y(t).с нулевыми начальными значениями. В теории управления соотношение (1) принято изображать графически (см. рис.).

Пусть, напр., система управления описывается линейным обыкновенным дифференциальным уравнением с постоянными коэффициентами

(2) (в реальных системах, как правило, ). Тогда

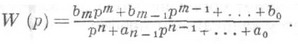(3)

Это же выражение можно получить, если, используя операторную форму записи уравнения (2) с помощью оператора дифференцирования р

определить П. ф. как отношение входного оператора системы В(р) к собственному оператору системы (р). П. ф. (3) системы (2) допускает следующее толкование: если выбрать управление , где s - комплексное число такое, что , то линейное неоднородное уравнение (2) имеет частное решение .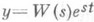

П. ф. не следует путать с переходной функцией, к-рая представляет собой отклик системы на воздействие единичной ступенчатой ф у н к ц и и

при нулевых начальных условиях.

П. ф. является одним из основных понятий теории линейных стационарных систем управления. Она не зависит от характера приложенных к системе управляющих воздействий, а определяется лишь параметрами самой системы и дает тем самым ее динамич. характеристику. Особую роль в теории управления играет функция W(iw) чисто мнимого аргумента, наз. амплитудно-фазовой, или частотной, характеристикой системы. Понятие П. ф. обобщается и на линейные системы управления иных типов (матричные, нестационарные, дискретные, с распределенными параметрами и др.).

Лит.:[1]Ройтенберг Я. Н., Автоматическое управление, 2 изд., М., 1978; [2] Математические основы теории автоматического регулирования, М., 1971; [3] Калман Р., Фалб П., Арбиб М., Очерки по математической теории систем, пер. с англ., М., 1971; [4] Бутковский А. Г., Характеристики систем с распределенными параметрами. Справочное пособие, М., 1979. Н. X. Розов.