- ПАРСЕВАЛЯ РАВЕНСТВО
- равенство, выражающее квадрат нормы элемента в векторном пространстве со скалярным произведением через квадраты модулей коэффициентов Фурье этого элемента по нек-рой ортогональной системе элементов; так, если X - нормированное сепарабельное векторное пространство со скалярным произведением
- соответствующая ему норма и 
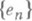- ортогональная в Xсистема, 
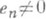, n=1,2,..., то равенством Парсеваля для элемента 
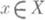наз. равенство
(1)
где
, n=1, 2,...,- коэффициенты Фурье
элемента хпо системе
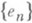. Если эта система 
ортонормирования, то П. р. имеет вид
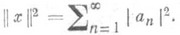
Выполнение П. р. для данного элемента
является необходимым и достаточным условием того, чтобы ряд Фурье этого элемента по ортогональной системе 
сходился к самому элементу хпо норме пространства X. Выполнение П. р. для любого элемента 
является необходимым и достаточным условием для того, чтобы ортогональная система 
была полной системой в X. Отсюда следует, в частности: если X - сепарабельное гильбертово пространство и 
- его ортонормированный базис, то П. р. по системе 
выполняется для каждого элемента 
; если X- сепарабельное гильбертово пространство, 
- ортонормированный базис в X,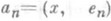 
и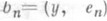 
- коэффициенты Фурье соответственно элементов х и у, то справедливо равенство
(2)
наз. обобщенным равенством Парсеваля. В достаточно законченном виде вопрос о полноте систем функций, являющихся собственными функциями дифференциальных операторов, был изучен В. А. Стендовым [1].
П. р. обобщается и на случай несепарабельных гильбертовых пространств: если
нек-рое множество индексов), является полной ортонормированной системой гильбертова пространства X, то для любого элемента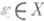 
справедливо П. р.
причем сумма в правой части равенства понимается как
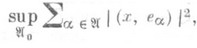
где верхняя грань берется по всевозможным конечным подмножествам
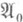множества 
В случае, когда
состоит из действительных функций, квадрат к-рых интегрируем по Лебегу на отрезке 
, в качестве полной ортогональной системы взята тригонометрич. система функций и
равенство (1) имеет вид
и наз. классическим равенством Парсеваля; оно было указано М. Парсевалем (М. Parseval, 1805). Если
и
то равенство, аналогичное формуле (2), выглядит следующим образом:
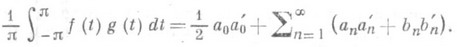(3)
Классы К т К' действительных функций, определенных на отрезке
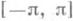, такие, что для всех 
и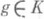 
имеет место обобщенное П. р. (3), наз. дополнительными. Примером дополнительных классов являются пространства 
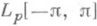и
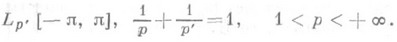
Лит.:[1] Стеклов В. А., "Записки физико-математич. общества", сер. 8, 1904, т. 15, № 7, с. 1-32; [2] Никольский С. М., Курс математического анализа, 2 изд., т. 2, М., 197й; [3] Ильин В. А., Позняк Э. Г., Основы математического анализа, 2 изд., ч. 2, М., 1980; [4] "Бари Н. К., Тригонометрические ряды, М., 1961; [5] Зигмунд А., Тригонометрические ряды, пер. с англ., т. 1, М., 1965; [6] Кириллов А. А., Гвишиани А. Д., Теоремы и задачи функционального анализа, М., 1979. Л. Д. Кудрявцев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
