ОКРУЖНОСТЬ

- замкнутая плоская кривая, все точки к-рой одинаково удалены от данной точки (ц е н т р а О.), лежащей в той же плоскости, что и кривая. О. с общим центром наз. концентрическими. Отрезок R, соединяющий центр О. с какой-либо ее точкой (а также длина этого отрезка), наз. р а д и у с о м О. Уравнение О. в прямоугольных декартовых координатах:

(x-a)²+(y-b)² = R²,

где а и b - координаты центра.

Прямая, проходящая через две точки О., наз. с е к у щ е й; отрезок ее, лежащий внутри О.,- хордой. Хорды, равноотстоящие от центра, равны. Хорда, проходящая через центр О., наз. ее диаметром. Диаметр, перпендикулярный к хорде, делит ее пополам.

Каждая из двух частей, на к-рые две точки О. делят ее, наз. дугой.

Угол, образованный двумя радиусами О., соединяющими ее центр с концами дуги, наз. центральным углом, а соответствующая дуга - дугой, на к-рую он опирается. Угол, образованный двумя хордами с общим концом, наз. вписанным углом. Вписанный угол равен половине центрального угла, опирающегося на дугу, заключенную между концами вписанного угла. Длина окружности С=2pR, длина дуги

, где а°- величина (в градусах) соответствующего центрального угла, a - его радианная мера.

Если через какую-либо точку плоскости провести к О. несколько секущих, то произведение расстояний от точки до обеих точек пересечения каждой секущей с О. есть постоянное число (для данной точки), в частности, оно равно квадрату длины отрезка касательной к О. из этой точки (степень точки). Совокупность всех точек плоскости, относительно к-рых данная точка имеет одинаковую степень, составляет связку О. Совокупность всех общих О. двух связок, лежащих в одной плоскости, наз. пучком О.

Часть плоскости, ограниченная О. и содержащая ее центр, наз. кругом. Сектором наз. часть круга, ограниченная дугой О. и радиусами, проведенными в концы этой дуги. Сегментом наз. часть круга, заключенная между дугой и ее хордой.

Площадь круга S=pR², площадь сектора S₁= 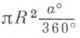, где а° - градусная мера соответствующего центрального угла, площадь сегмента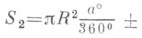 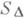, где S_D -площадь треугольника с вершинами в центре круга и в концах радиусов, ограничивающих соответствующий сектор, знак "-" берется, если а°<180°, и знак "+", если а°>180°.

О. на выпуклой поверхности локально почти изоме-трична границе выпуклой поверхности конуса (теорема Залгаллера). О. в многообразии ограниченной кривизны может иметь достаточно сложное строение (т. е. могут существовать угловые и кратные точки, О. может состоять из нескольких компонент и т. п.). Тем не менее точки О. в многообразиях ограниченной кривизны можно естественно упорядочить, превратив ее тем самым в циклически упорядоченное множество (см. [1]).

Об О. в более общих пространствах - банаховых, финслеровых и т. п. см. в ст. Сфера.

Лит.:[1] Энциклопедия элементарной математики, кн. 4, М., 1963; [2] "Тр. Матем. ин-та АН СССР", 1965, т. 76, с. 88-114.

А. Б. Иванов.