- ОГИБАЮЩАЯ
семейства кривых на плоскости - кривая, к-рая в каждой точке касается одной из кривых семейства, причем касания вдоль О. переходит от одной кривой семейства к другой. Напр., для семейства окружностей одинакового радиуса с центрами на прямой О. состоит из двух параллельных прямых. Если С- параметр семейства, t- параметр вдоль О., С(t)- значение Сдля одной из кривых семейства, касающихся О. в точке с параметром t, то предполагается возможность выбора С(t)так, что функция С(t)ни на каком участке изменения tне постоянна.
Для семейства кривых, заданного уравнением
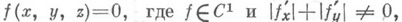необходимым признаком существования О. является выполнение при 
условий
Система (1) служит для нахождения точек О., но (1) могут удовлетворять и другие особые точки. семейства. Достаточным признаком точек О. является
и выполнение, кроме (1), условия
Для семейства плоских кривых, заданных
-гладкой функцией
где
- параметр семейства, 
- параметр вдоль его кривых, необходимым признаком точек О. является 
или, что то же,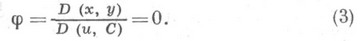
Достаточным признаком является
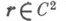и выполнение, кроме (3), условия
Нарушение условий (2), (4) чаще всего связано с появлением на О. точки возврата.
Для зависящего от одного параметра С семейства поверхностей в пространстве О. есть поверхность, к-рая в каждой ее точке с внутренними параметрами
касается поверхности семейства с параметром 
, причем функция 
ни в какой области изменения 
не постоянна. Напр., для сфер одинакового радиуса с центрами на прямой О. является цилиндром. Для семейства, заданного уравнением
необходимым признаком О. является система равенств
а достаточным:
и выполнение, кроме (5), условий
Для семейства
необходимым признаком О. служит равенство
а достаточным:
и выполнение, кроме (7), условий
С нарушением первых из условий (6), (8) чаще всего связано появление на О. ребра возврата. Линию касания О. с одной поверхностью семейства наз. характеристикой. Ребро возврата на О. в свою очередь обычно является О. характеристик.
Для зависящего от двух параметров A, B семейства поверхностей в пространстве О. есть поверхность, касающаяся в каждой своей точке
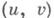поверхности семейства с параметрами 
причем ни в какой области изменения 
не существует такой функции 
что 
Для семейства, заданного уравнением 
, где 
необходимым признаком О. является система
а достаточным:
и выполнение, кроме (9), условий
Для семейства
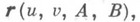где 
и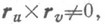 
необходимым признаком О. служит система
а достаточным:
и выполнение, кроме (10), условий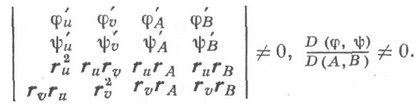
Более сложное понятие О. для зависящего от kпараметров семейства m-мерных подмногообразий в n-мерном многообразии вводится (см. [1]) на основе теории особенностей дифференцируемых отображений как специальный вид особенности семейства.
Лит.:[1] 3алгаллер В. А., Теория огибающих, М., 1975; [2] Фавар Ж., Курс локальной дифференциальной геометрии, пер. с франц., М., 1960; [3] Толстов Г. П., "Успехи матем. наук", 1952, т. 7, в. 4, с. 173-79.
В. А. Залгаллер.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
