НОРМЕННЫИ ВЫЧЕТ

символ нор мен-ног о вычета, символ Гильберта,- функция, сопоставляющая упорядоченной паре элементов х, у мультипликативной группы нек-рого локального поля К элемент являющийся корнем из единицы. Эта функция может быть определена следующим образом. Пусть - нек-рый первообразный корень степени пиз единицы. Максимальное абе-лево расширение Lполя Kс группой Галуа 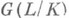показателя пполучается присоединением к Ккорней для всех 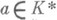. С другой стороны, существует кано-нич. изоморфизм (основной изоморфизм локальной полей классов теории)

Норменный вычет для пары х, у определяется из соотношения

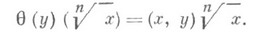
В частном случае, для квадратичных полей, понятие символа Н. в. было введено Д. Гильбертом (D. Hilbert). Существует явное и использующее только локчльную теорию полей классов определение Н. в. [4]. Свойствасимвола :

1)билинейность:

2) кососимметричность:

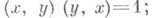
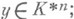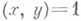3) невырожденность: из для всех следует, что из для всех 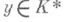следует, что ;

4) если

5) если - автоморфизм поля К, то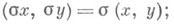

6)пусть- конечное расширение поля 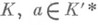и .

Тогда где в левой части формулы символ Н. в. рассматривается для поля 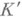, в правой части - для ноля , а - норменное отображение из K' в K.

7) из 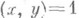следует, что уявляется нормой из расширения 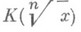(это свойство дало название символу).

Функция (x, у)индуцирует невырожденное билинейное спаривание

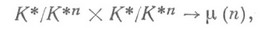
где - группа корней из единицы, порожденная 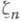. Пусть задано отображение в некоторую абелеву группу А, удовлетворяющее условиям 1), 4) и условию непрерывности: для любого множество замкнуто в 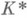. Символ Н. в. обладает следующим свойством универсальности [3]: существует гомоморфизм 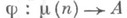такой, что для любых

Это свойство служит основой аксиоматич. определения Н. в.

Если F- глобальное поле,a К- пополнение поля Fотносительно нек-рой точки v, то символом Н. в. называют также функцию определенную на , получающуюся композицией (локального) символа Н. в.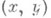с естественным вложением .

Иногда символом Н. в. наз. автоморфизм q(x) максимального абелева расширения поля К, соответствующий элементу в силу локальной теории полей классов.

Лит.:[1] Алгебраическая теория чисел, пер. с англ., М., 1969; [2] Кох X., Теория Галуа р-расширений, пер. с нем., М., 1973; [3] Милнор Дж., Введение в алгебраическую К-теорию, пер. с англ., М., 1974; [4] Шафаревич И. Р., "Матем. сб.", 1950, т. 26, №1, с. 113-46.

Д. В. Кузьмин.