НЕРОНА МОДЕЛЬ

абелева многообразия - групповая схема, сопоставляемая абелеву многообразию и обладающая нек-рым свойством минимальности. Если R- локальное гензелево кольцо дискретного нормирования с полем вычетов ки полем частных К, А- абелево многообразие размерности dнад полем А, то моделью Нерона многообразия Аназ. гладкая коммутативная групповая схема над кольцом R, общий слой к-рой - изоморфен многообразию А, а канонич. гомоморфизм является

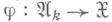изоморфизмом. Это понятие было введено А. Нероном [1] в случае совершенного поля к. В локальном случае Н. м. существует и определена однозначно с точностью до R-изоморфизма. Н. м. обладает следующим свойством минимальности: для любой гладкой R-схемы и любого морфизма общих слоев существует однозначно определенный морфизм R-схем, индуцирующий морфизм . Если S- одномерная регулярная нётерова схема, - ее общая точка,- ее канонич. вложение, А- абелево многообразие над , то Н. м. многообразия Аопределяется как гладкая квазипроективная групповая схема над S, представляющая пучок 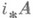относительно плоской топологии Гротендика на S(см. [4]).

Об обобщении понятия Н. м. на произвольные схемы см. [3].

Лит.:[1] Nёrоn A., Modules minimaux des varietes abiiliennes sur les corps locaux et globaux, P., 1964 (Publ. Math. INES, N 21); [2] Mазур В., "Математика", 1973, т. 17, № 2, с. 3-57; [3] Rауnaud M., "С. r. Acad. sci., Ser. A.", 1966, t. 262, p. 345-47; [4] его же, в кн.: Dix exposes sur la cohomologie des schemas, Amst.- P., 1968, p. 12-30; [5] Groupes de monodromie en geometrie algebrique, v. 1, В., 1972.