- МОНОТОННАЯ ФУНКЦИЯ
-функция одного переменного, определенная на нек-ром подмножестве действительных чисел, приращение к-рой
 при
при  не меняет знака, т. е. либо всегда неотрицательно, либо всегда неположительно. Если
не меняет знака, т. е. либо всегда неотрицательно, либо всегда неположительно. Если 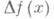 строго больше (меньше) нуля, когда
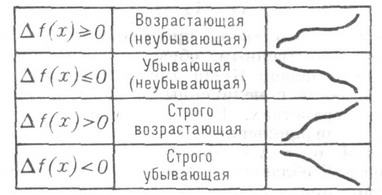
строго больше (меньше) нуля, когда  то М. ф. наз. строго монотонной (см. Возрастающая функция, Убывающая функция). Различные типы М. ф. представлены в таблице.
то М. ф. наз. строго монотонной (см. Возрастающая функция, Убывающая функция). Различные типы М. ф. представлены в таблице.Если функция f в каждой точке нек-рого промежутка имеет производную, к-рая не меняет знака (соответственно сохраняет постоянный знак), то функция f монотонна (строго монотонна) на этом промежутке.
Понятие М. ф. действительного переменного обобщается на функции различных классов. <Напр.,функция
 , определенная на
, определенная на 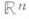 , наз. монотонной, если из условия
, наз. монотонной, если из условия  следует, что всегда
следует, что всегда  или всегда
или всегда 
 Подобным же образом определяется М. ф. алгебры логики.
Подобным же образом определяется М. ф. алгебры логики.М. ф. многих переменных, возрастающие или убывающие относительно нек-рой точки, определяются следующим образом. Пусть функция f определена на п- мерном замкнутом кубе

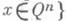 - множество уровня функции f. Функция f наз. возрастающей (соответственно убывающей) относительно точки
- множество уровня функции f. Функция f наз. возрастающей (соответственно убывающей) относительно точки  , если для любого числа tи любой точки
, если для любого числа tи любой точки 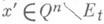 , не отделенной в кубе
, не отделенной в кубе 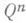 множеством
множеством 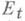 от
от 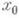 , имеет место
, имеет место 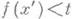 (соответственно
(соответственно  ), а для любой точки
), а для любой точки 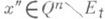 , отделенной в кубе
, отделенной в кубе  множеством
множеством 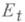 от
от  , имеет место
, имеет место 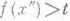 (соответственно
(соответственно  ). Функции, возрастающие или убывающие относительно нек-рой точки, наз. монотонными относительно этой точки.
). Функции, возрастающие или убывающие относительно нек-рой точки, наз. монотонными относительно этой точки.Л. Д. Кудрявцев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
