МОНОМИАЛЬНОЕ ПРЕДСТАВЛЕНИЕ

конечной группы G - такое представление группы Gв конечномерном векторном пространстве V, что в нек-ром базисе этого пространства матрица 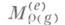оператора для любого элемента имеет точно один ненулевой элемент в каждой строке и в каждом, столбце. Иногда М. п. наз. непосредственно матричное представление . М. п. является частным случаем импримитивного представления (см. Импримитивная группа). А именно, набор одномерных подпространств в V, порожденных векторами является системой импримитивности для . Наоборот, если для нек-рого представления 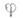группы Gв векторном пространстве существует система импримитивности, состоящая из одномерных подпространств, то - М. п. Пусть Н- какая-либо подгруппа в . Примером М. п. может служить представление G, индуцированное каким-нибудь одномерным представлением подгруппы Н(см. Индуцированное представление). Такие представления наз. также индуцированными М. п. (см. [1]). Не всякое М. п. является индуцированным М. п. (однако, если М. п.неприводимо, то оно будет индуцированным М. п.). Данное выше определение М. п. возникло в классич. теории представлений конечных групп. Часто, однако, это определение изменяют, называя М. п. произвольное представление группы G, индуцированное одномерным представлением какой-либо подгруппы H в G. Втаком виде определение М. п. имеет смысл уже не только для конечных групп и их конечномерных представлений, но и, напр., для групп Ли и их представлений в гильбертовых пространствах (подгруппа Нпри этом предполагается замкнутой). Для достаточно широкого класса групп конструкция М. п. оказывается достаточной для описания всех унитарных неприводимых представлений. А именно, группы, все унитарные неприводимые представления к-рых мономиальны, наз. мономиальными группами, или М- группами. К их числу относятся, напр., все конечные нильпотентные группы и все связные нильпотентные группы Ли. Все конечные М-группы, а также все мономиальные группы Ли разрешимы (см. [2]).

Лит.:[1] Кэртис Ч., Райнер И., Теория представлений конечных групп и ассоциативных алгебр, пер. с англ., М., 1969; [2] Кириллов А. А., Элементы теории представлений, 2 изд., М., 1978.

В. Л. Попов.