МОНОГЕННОСТИ МНОЖЕСТВО

- множество всех производных чисел данной функции комплексного переменного в данной точке. Точнее, пусть Е- множество на комплексной плоскости - неизолированная его точка, f(z)- комплекснозначная функция переменного . Комплексное число а(собственное или равное 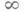) наз. производным числом функции 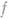в точке 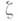относительно множества Е, если существует последовательность z_n ОE со свойствами: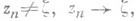

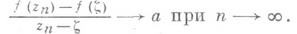
Множество 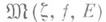всех производных чисел функции f в точке 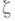относительно Еназ. множеством моногенности функции f в точке относительно Е(см. [1]). Множество состоит из единственной конечной точки атогда и только тогда, когда 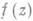- моногенная функция в точке 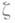относительно Еи 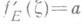. Множество 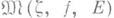всегда замкнуто, и для каждого замкнутого множества Арасширенной комплексной плоскости 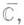каждого множества 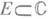и каждой конечной неизолированной точки 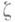этого множества найдется такая функция 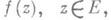что Если 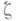- внутренняя точка Е, то для любой непрерывной в нек-рой окрестности этой точки функции 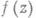множество является 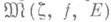замкнутым и связным (континуумом) на 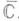, и обратно, для любого континуума найдется функция , непрерывная в нек-рой окрестности 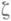, для к-рой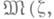 Если функция 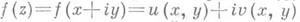дифференцируема по совокупности действительных переменных во внутренней точкемно 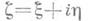жества Е, то представляет собой окружность 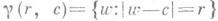(возможно, вырожденную и точку при r=0) с центром и радиусом где

- т. н. формальные производные. Верно и обратное: каждая окружность является М. м. для нек-рой функции f, дифференцируемой по ( х, у )в заданной внутренней точке множества Е.

Если f(z)непрерывна в области G, то почти в каждой точке множество есть либо нек-рая окружность (см. [2]). В общем случае произвольного (необязательно измеримого) множества Ен произвольной (необязательно измеримой) конечной функции 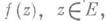почти в каждой точке имеет место один из следующих трех случаев: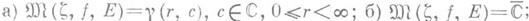

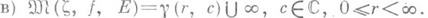
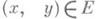При этом почти в каждой точке дифференцируемости функции по совокупности выполнен случай а), почти же в каждой точке непрерывности функции f(z) - один из первых двух случаев. Каждый из случаев а) - в) в отдельности может реализоваться почти в каждой точке

Лит.:[1] Федоров В. С, "Успехи матем. наук", 1952, т. 7, в. 2, с. 7-16; [2] Трохимчук Ю. Ю., Непрерывные отображения и условия моногенности, М., 1963; [3] Долженко Е. П., "Изв. АН СССР. Сер. матем.", 1962, т. 26, с. 347-60.

Е. П. Долженко.