МАССОВОГО ОБСЛУЖИВАНИЯ СИСТЕМА

входящий поток вызовов - случайный процесс, заданный тем или иным образом и описывающий поступление вызовов в систему обслуживания. Входящий поток определяется обычно случайной последовательностью где указывают интервалы между поступлениями в систему групп требований объемов соответственно Если то поток наз. ординарным. Эквивалентным образом входящий поток можно задавать с помощью точечного процесса или процесса {e(t); }, указывающего количество вызовов, поступивших в систему к моменту времени t. Можно считать для определенности, что e(t)=e(t-0).

Наиболее распространенное требование, к-рое обычно предъявляется к входному потоку, состоит в его стационарности. Это условие может быть двояким: либо требуется стационарность в узком смысле последовательности (обозначается либо требуется, чтобы процесс e(t).был процессом со стационарными в узком смысле приращениями (обозначается Эти два требования, вообще говоря, не совпадают.

Интенсивностью стационарного потока наз. число

Если

то

так что m равно среднему числу вызовов, поступивших в систему за единицу времени. Если последовательность стационарна и эргодична и то

В остальных случаях связь m с распределением последовательности может быть более сложной. Пусть дан процесс с интенсивностью m и с начальным значением е(0)=0. С числом m тесно-связан другой параметр входного потока, определяемый равенством

Этот предел всегда существует и Если

то тогда и только тогда, когда входной поток ординарен.

При изучении свойств входного потока часто используются т. н. функции Пальма

(здесь е(0)=0), к-рые имеют смысл условных вероятностей того, что на интервале (0, t).появится kвызовов при условии, что в момент времени 0 пришел вызов. С распределением е(t).функции j_k (t).связаны равенствами

Если

то

Значительную роль в теории массового обслуживания играют т. н. простейшие, или пуассоновские, входные потоки - стационарные входные потоки, для к-рых 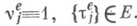Чтобы определить простейший поток в терминах процесса e(t), требуют, чтобы процесс {e(t)}был пуассоновским. Приращения этого процесса на непересекающихся интервалах времени независимы и имеют распределение-Пуассона с параметрами, пропорциональными длинам интервалов.

Находят широкое применение (особенно в телефонии) также и неоднородные пуассоновские потоки, к-рые характеризуются процессами е(t).с независимыми приращениями, распределенными по закону Пуассона

где A(t) - ведущая функция процесса (в однородном случае ).

Особая роль пуассоновских процессов в теории массового обслуживания во многом объясняется основной предельной теоремой для входящих потоков, к-рая устанавливает, что в широких предположениях сумма большого числа произвольных независимых стационарных входных потоков малой интенсивности сходится к пуассоновскому процессу. Частое использование предположения о том, что входной поток пуассоновский, обусловливается тем, что во многих приложениях реальные входные потоки образуются именно таким способом (напр., поток вызовов, поступающих на телефонную станцию, представляет собой сумму слабых потоков, исходящих от отдельных абонентов).

Ниже приведена основная предельная теорема в двух формах. Первая относится к суммам произвольных (нестационарных) входных потоков.

Пусть даны возрастающие вместе с псовокупности независимых процессов зависящих от параметра n (т. е. рассматривается схема серий), п введены следующие обозначения

Пусть, кроме того, при любом фиксированном t>0 выполнено условие

при равномерно по т(это и есть условие малой интенсивности потоков ). Тогда, для того чтобы конечномерные распределения процесса

сходились к распределениям пуассоновского процесса с ведущей функцией A.(t), необходимо и достаточно, чтобы при

Если в рассматриваемой схеме серий, процессы и ординарны, то имеет место также следующее утверждение. Пусть 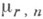- интенсивность и при

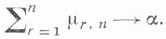
Тогда для сходимости конечномерных распределений процессов е _п(t).к распределениям пуассоновского процесса е(t).с параметром aнеобходимо и достаточно, чтобы при каждом t

где 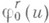- функция Пальма для процесса 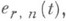определенная равенством (1). Если при

равномерно по г, то условие (2) очевидно будет выполнено.

Лит. см. при ст.. Массового обслуживания теория.

А. А. Боровков.