- ЛОКАЛЬНОЕ ПОЛЕ
- полное дискретно нормированное поле с конечным полем вычетов. Структура Л. п. хорошо известна: 1) если характеристика Кравна 0, то Кявляется конечным расширением поля
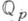р-адических чисел;2) если характеристика Кбольше 0, то K изоморфно полю k((T)).формальных степенных рядов над конечным полем k. Локальными такие поля называются в противоположность глобальным полям (конечным расширениям полей 
или k(T)).и являются средством изучения последних. О когомологич. свойствах расширений Галуа локадьных полей см. [1], а также ст. Адель и Полей классов теория.
Для построения теории полей классов многомерных схем используется обобщение понятия Л. п. А именно, структурой п- мерного локального поля наз. последовательность O0, О 1, . .., О п полных колец дискретного нормирования вместе с изоморфизмами
где k - поле вычетов, а К - поле частных кольца О;при этом k(On).должно быть конечным. Для n-мерных Л. п. построена структурная теория (см. [3]).
Лит.:[1] Serre J.-P., Corps locaux, P., 1962; [2] Алгебраическая теория чисел, пер. с англ., М., 1969; [3] Паршин А. Н., "Докл. АН СССР", 1978, т. 243, № 4, с. 855 - 58.
В. И. Данилов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
