ЛЕМНИСКАТНЫЕ ФУНКЦИИ

лемнискатические функции, - частный случай эллиптических функций, возникающий при обращении эллиптич. интеграла частного вида

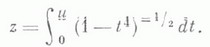
Эти интегралы появились впервые при вычислении длины дуги Бернулли лемнискаты в работах Дж. Фаньяно (G. Fagnano, 1715). Сами Л. ф. ввел К. Гаусс (С. Gauss, 1797). Л. ф. две:

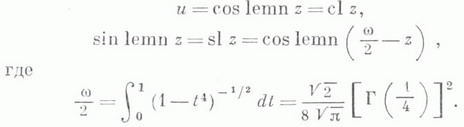
Л. ф. выражаются через Якоби эллиптические функции

с модулем

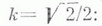
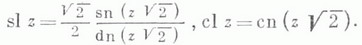
В теории Вейерштрасса эллиптических функций Л. ф. появляются вт. н. гармоническом случае, когда инварианты g₂=4, g₃=0.

Лит.:[1] Уиттекер Э.-Т., В а т с о н Д. Н., Курс современного анализа, пер. с англ., 2 изд., ч. 2, М., 1963, гл. 22.

Е. Д. Соломенцев.