- КООПЕРАТИВНАЯ ИГРА
- нестратегическая игра (см. Игр теория), задаваемая тройкой (I, u, H), где I - множество (обычно конечное), элементы к-рого наз. игроками, а подмножества
- коалициям и, v- вещественная функция, определенная на множестве коалиций и называемая характеристической функцией игры, Н- некоторое подмножество векторов Х I (компоненты х i к-рых соответствуют игрокам iиз I), называемых дележам и. К. и. впервые были введены Дж. Нейманом (J. Neumann, 1929) как аппарат кооперативной теории (бескоалиционных) игр.В классической теории К. и. принимается:
На множестве Нвводится бинарное отношение
доминирования (предпочтения) дележей по коалиции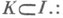 
Если
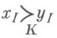для нек-рого 
то полагают 
Относительно этого отношения доминирования формулируются понятия оптимальности дележей.
Значительная часть содержания теории К. и. состоит в разработке понятий оптимальности, в доказательствах их реализуемости для различных частных классов К. и. и фактическом нахождении таких реализаций. К числу принципов оптимальности, разрабатываемых применительно к К. п., относятся: двойная (т. е. внешняя и внутренняя) устойчивость, реализуемая в форме решений по Нейману - Моргенштерну (Н-М-решения); недоминируемость дележей (см. Ядра в теории игр); устойчивость относительно угроз; устойчивость в смысле минимизации наибольшей неудовлетворенности (см. Устойчивость в теории игр), справедливость (см. Щепли вектор )и др.
Введение на классе К. и. алгебраич. операций приводит к исчислениям К. и. и к исследованию взаимосвязей между этими операциями и различными принципами оптимальности. Специальному изучению подвергались различные частные классы К. и., описанные ниже.
Простая игра - К. и., в к-рой характеристич. функция vпринимает ровно два значения (обычно 0 и 1); при этом коалиции К, на к-рых достигается максимальное значение v(K), наз. выигрывающими. Частным случаем простых игр является взвешенная мажоритарная игра, в к-рой коалиция Кявляется выигрывающей, если
>
где 
- некоторые заданные числа.Сбалансированная игра - К. и., для характеристической функции которой
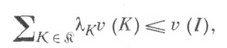
если семейство коалиций
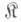и числа 
таковы,что
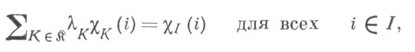
где cK(i)= 1, если
и 0 в противном случае.Сбалансированные игры и только они имеют непустое с-ядро.
Выпуклая игра - К. п., для характеристич. функции к-рой при К,
В выпуклой игре с-ядро непусто и совпадает с единственным Н - М-решением. Если К. п. строго выпуклая (т. <е. неравенство (*) строгое), то вектор Шегога является центром тяжести с-ядра.
Игра с квотой - К. и. с характеристич. функцией v, для к-рой существует такой вектор
, что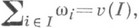 
и для любых игроков 
имеет место u({i, j})= wi+wj.Игра рынка - К. и., порожденная рынком, к-рый понимается как система
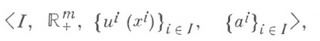
где I - множество участников рынка (с ттоварами),
- начальный набор товаров г-го участника, и i( х i)- функция полезности г-го участника, определенная на 
. На основе этого рынка строится К. и., в к-рой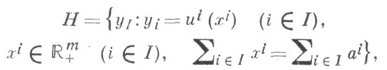
а характеристич. функция определяется равенством
Теория классич. К. и. подвергалась обобщениям в различных направлениях (см. также Неатомическая игра).
Игры без побочных платежей - нестратегич. игры, задаваемые тройкой (I, u, Н), где v(в отличие от классических К. и.) - функция, к-рая каждой коалиции Кставит в соответствие множество v(K)векторов Х I, удовлетворяющее условиям: 1) u(K)замкнуто и выпукло; 2) если xI Оu(K)и yi<xi(iОK), то
3) если 
то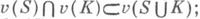 
4)
для всех 
5) 
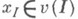тогда и только тогда, когда 
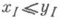для нек-рого 
Доминирование в игре без побочных платежей определяется следующим образом:
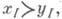если существует такая непустая коалиция 
что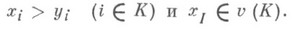 
Игра в форме функции разбиения- нестратегическая игра, задаваемая множеством игроков I и функцией v, к-рая каждому разбиению
=( Р 1, . . ., Р п )множества I ставит в соответствие вектор 
. Максимальный выигрыш, к-рый может гарантировать себе коалиция К, определяется формулой 
Дележ в игре в форме функции разбиения определяется как вектор х р удовлетворяющий условиям: 
=
для нек-рого. Дележ xI доминирует дележ у I по коалиции К, если: xi> у i(
); 
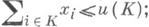существует такое 
, что
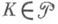и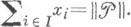 
Лит.:[1] Нейман Дж., Моргенштерн О., Теория игр и экономическое поведение, пер. с англ.,М., 1970; [2] Воробьев Н. Н., "Успехи матем. наук", 1970, т. 25, № 2, с. 81-140; [3] Розенмюллер И., Кооперативные игры и рынки, пер. с англ., М., 1974.
Н. Н. Воробьев, А. И. Соболев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
