- КОЛЬЦЕВАЯ ГРАНИЦА
- подмножество Г пространства MA максимальных идеалов коммутативной банаховой алгебры А с единицей над полем С комплексных чисел, на к-ром модули Гелъфанда представлений а всех элементов
 достигают максимума. Напр., можно положить Г=М A (тривиальная граница). Интерес представляют нетривиальные границы с тем или иным свойством минимальности. Среди замкнутых границ
достигают максимума. Напр., можно положить Г=М A (тривиальная граница). Интерес представляют нетривиальные границы с тем или иным свойством минимальности. Среди замкнутых границ  существует минимальная дМ A- такая замкнутая граница, что
существует минимальная дМ A- такая замкнутая граница, что  для каждой замкнутой границы Г; она наз. границей Шилова. Точки границы Шилова характеризуются тем, что для каждой окрестности
для каждой замкнутой границы Г; она наз. границей Шилова. Точки границы Шилова характеризуются тем, что для каждой окрестности  такой точки xи каждого е>0 существует элемент
такой точки xи каждого е>0 существует элемент  для к-рого max|а| = 1 и
для к-рого max|а| = 1 и  вне V. Точки
вне V. Точки  составляют "наиболее устойчивую" часть множества М A максимальных идеалов: если В- коммутативное банахово расширение алгебры А, то максимальные идеалы (мультипликативные функционалы), отвечающие таким точкам, расширяются до максимальных идеалов (мультипликативных функционалов) алгебры В, тогда как за пределами дМ A такое расширение, вообще говоря, невозможно. Это обстоятельство аналогично устойчивости границы спектра ограниченного линейного оператора банахова пространства. Типичный пример: алгебра Асостоит из непрерывных функций в диске
составляют "наиболее устойчивую" часть множества М A максимальных идеалов: если В- коммутативное банахово расширение алгебры А, то максимальные идеалы (мультипликативные функционалы), отвечающие таким точкам, расширяются до максимальных идеалов (мультипликативных функционалов) алгебры В, тогда как за пределами дМ A такое расширение, вообще говоря, невозможно. Это обстоятельство аналогично устойчивости границы спектра ограниченного линейного оператора банахова пространства. Типичный пример: алгебра Асостоит из непрерывных функций в диске  аналитических при |l|<1. В этом случае М A отождествляется с замкнутым диском, а дМ A- с его топологич. границей; максимальные идеалы, отвечающие внутренним точкам диска, не продолжаются до максимальных идеалов алгебры всех непрерывных функций на границе, в к-руго естественно (согласно принципу максимума) вкладывается А, а максимальные идеалы, отвечающие граничным точкам,- продолжаются.
аналитических при |l|<1. В этом случае М A отождествляется с замкнутым диском, а дМ A- с его топологич. границей; максимальные идеалы, отвечающие внутренним точкам диска, не продолжаются до максимальных идеалов алгебры всех непрерывных функций на границе, в к-руго естественно (согласно принципу максимума) вкладывается А, а максимальные идеалы, отвечающие граничным точкам,- продолжаются.Подобно алгебрам аналитич. функций, для общих коммутативных банаховых алгебр имеет место локальный принцип максимума модуля: если V- открытое подмножество пространства Мд, то

для всех
 где-
где-  замыкание п дV- топологич. граница множества Vв М A. Грубо говоря, это означает, что точка локального максимума непременно является точкой глобального максимума (нек-рого, быть может, другого элемента).
замыкание п дV- топологич. граница множества Vв М A. Грубо говоря, это означает, что точка локального максимума непременно является точкой глобального максимума (нек-рого, быть может, другого элемента).Понятие К. г. используется при изучении равномерных алгебр, т. е. замкнутых, разделяющих точки и содержащих константы подалгебр Аалгебры С(X)всех непрерывных функций на компакте X. В данной ситуации
 Для каждой точки
Для каждой точки существует представляющая мера, сосредоточенная на границе Шилова, т. е. такая вероятностная мера m, что
существует представляющая мера, сосредоточенная на границе Шилова, т. е. такая вероятностная мера m, что
при всех
 (это верно для произвольных коммутативных банаховых алгебр). В простейшем (описанном выше) случае диска и алгебры аналитич. функций последняя формула сводится к Пуассона формуле. Вообще говоря, представляющая мера m не единственна. Для точек x, принадлежащих одной и той же доле Глисона (см. Алгебра функций), меры m можно выбирать взаимно абсолютно непрерывными, что при нек-рых дополнительных условиях типа единственности представляющих мер позволяет наделять доли Глисона пространства максимальных идеалов одномерной аналитич. структурой, согласованной с алгеброй. Каждая точка границы Шилова равномерной алгебры составляет одноточечную долю Глисона, но обратное, вообще говоря, неверно.
(это верно для произвольных коммутативных банаховых алгебр). В простейшем (описанном выше) случае диска и алгебры аналитич. функций последняя формула сводится к Пуассона формуле. Вообще говоря, представляющая мера m не единственна. Для точек x, принадлежащих одной и той же доле Глисона (см. Алгебра функций), меры m можно выбирать взаимно абсолютно непрерывными, что при нек-рых дополнительных условиях типа единственности представляющих мер позволяет наделять доли Глисона пространства максимальных идеалов одномерной аналитич. структурой, согласованной с алгеброй. Каждая точка границы Шилова равномерной алгебры составляет одноточечную долю Глисона, но обратное, вообще говоря, неверно.Равенство дМ А=Х = М А для равномерных алгебр служит простейшим необходимым условием совпадения Ас С(Х). Без дополнительных предположений оно не является достаточным для такого совпадения даже в случае алгебр A = R(X)равномерных пределов рациональных функций на плоском компакте X.
Пусть X- метризуемый компакт и А- равномерная алгебра на X. Тогда существует минимальная среди всех границ: д 0 М A. Замыкание минимальной границы совпадает с дМ A, однако, вообще говоря, д 0 М А не замкнуто: пример доставляет подалгебра тех аналитич. внутри диска
 функций, для к-рых f(0)=f(1). Граница д 0 М A совпадает с множеством точек пика относительно А, т. е. таких точек
функций, для к-рых f(0)=f(1). Граница д 0 М A совпадает с множеством точек пика относительно А, т. е. таких точек  для к-рых существует
для к-рых существует  с
с  при всех
при всех  С другой стороны, известно формально гораздо более слабое достаточное условие принадлежности к д 0 М A. Именно, если точка
С другой стороны, известно формально гораздо более слабое достаточное условие принадлежности к д 0 М A. Именно, если точка  такова, что при нек-рых 0<с<1 и
такова, что при нек-рых 0<с<1 и  для каждой окрестности Vточки x в Аимеется элемент а, для к-рого
для каждой окрестности Vточки x в Аимеется элемент а, для к-рого 
 и
и  при
при  то
то  Абстрактная формула Пуассона усиливается следующим образом: для любой точки
Абстрактная формула Пуассона усиливается следующим образом: для любой точки  существует представляющая мера, сосредоточенная на д 0 М A (при этом д 0 М A, есть Gd -множество), и в таком виде она с успехом применяется в нек-рых вопросах теории приближений. Точки
существует представляющая мера, сосредоточенная на д 0 М A (при этом д 0 М A, есть Gd -множество), и в таком виде она с успехом применяется в нек-рых вопросах теории приближений. Точки  характеризуются тем, что для них такая мера единственна и совпадает с d-мерой, т. е. минимальная граница есть частный случай границы Шоке.
характеризуются тем, что для них такая мера единственна и совпадает с d-мерой, т. е. минимальная граница есть частный случай границы Шоке.Для алгебры A = R(X)равномерных пределов рациональных функций на плоском компакте Xсовпадение Ас С(X)равносильно совпадению Х = Мд с д 0 М A. Для произвольных равномерных алгебр это не так: существует равномерная алгебра А, отличная от С( М A), для к-рой М A метризуемо, и каждая точка
 является точкой пика (т. е. д 0 М A = М A). Существует и такая равномерная алгебра, что все доли Глисона тривиальны (одноточечны), однако даже граница Шилова составляет собственную часть пространства максимальных идеалов.
является точкой пика (т. е. д 0 М A = М A). Существует и такая равномерная алгебра, что все доли Глисона тривиальны (одноточечны), однако даже граница Шилова составляет собственную часть пространства максимальных идеалов.Одно из алгебраич. обобщений понятия границы Шилова заключается в следующем. Пусть д 1 М A=дМ A и I - замкнутый идеал, порожденный набором элементов

 Пространство М А/I естественно отождествляется с множеством общих нулей функций
Пространство М А/I естественно отождествляется с множеством общих нулей функций  Замыкание объединения границ дМ А/1 по всем (п-1)-наборам обозначается д п М A. Напр., для алгебры непрерывных функций в бидиске
Замыкание объединения границ дМ А/1 по всем (п-1)-наборам обозначается д п М A. Напр., для алгебры непрерывных функций в бидиске 
 аналитических внутри его, д х М А- остов |l1| = | l2| = 1, д 2 М A- топологнч. граница |l1| = 1,
аналитических внутри его, д х М А- остов |l1| = | l2| = 1, д 2 М A- топологнч. граница |l1| = 1, 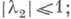
 |l2|=1, д 3 М А=М А. Эти обобщения полезны при доказательстве теорем о многомерной аналитич. структуре в пространстве максимальных идеалов.
|l2|=1, д 3 М А=М А. Эти обобщения полезны при доказательстве теорем о многомерной аналитич. структуре в пространстве максимальных идеалов.Понятия К. г. (или функциональных границ), аналогичные описанным, встречаются в теории аналитич. функций (граница Бергмана), теории вероятностей (граница Мартина) и в ряде других разделов математики. При этом исходный запас функциональных элементов не обязательно предполагается составляющим алгебру или кольцо.
Лит.:[1] Basener R., "Proc. Airier. Math. Soc", 1975, v. 47, № 1, p. 98-104; [2] Вrowder A., Introduction to function algebras, N. Y.- Amst., 1969; [3] Гамелин Т. В., Равномерные алгебры, пер. с англ., М., 1973; [4] Гельфанд И. М., Райков Д. А., Шилов Г. Е., Коммутативные нормированные кольца, М., 1960; [5] Гончар А. А., "Изв. АН СССР. Сер. матем.", 1963, т. 27, № 4 с. 949-55; [6] Фелпс Р., Лекции о теоремах Шоке, пер. с англ., М., 1968.
Е. А. Горин.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
