КОД С ИСПРАВЛЕНИЕМ АРИФМЕТИЧЕСКИХ ОШИБОК

код, исправляющий арифметические ошибки,- код, предназначенный для контроля работы сумматора. При сложении чисел, представленных в двоичной системе счисления, одиночный сбой в работе сумматора приводит, как правило, к изменению результата на нек-рую степень числа два. В связи с этим в кольце целых чисел Zвводится понятие (одиночной) арифметической ошибки как преобразования числа Nв число i=0, 1, ... . Функция r(N₁, N₂) на определяемая как минимальное число арифметич. ошибок, преобразующих N₁ в N₂, является метрикой. Произвольное конечное подмножество (код) характеризуется расстоянием

где минимум берется по всем различным 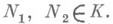Последовательности из tили менее арифметич. ошибок преобразуют любое число N в метрический шар радиуса tс центром в N. Поэтому если метрические шары радиуса t, описанные вокруг любых двух чисел кода, не пересекаются (т. е. расстояние кода больше 2t), то код наз. кодом, исправляющим tарифметических ошибок. Если же метрический шар радиуса s, описанный вокруг любого числа кода, не содержит других чисел кода (т. е. расстояние кода больше s), то код наз. кодом, обнаруживающим арифметических ошибок. Метрика р допускает другое описание: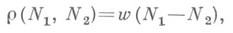

где w(N)- (арифметический) вес числа N, равный минимально возможному числу ненулевых коэффициентов в представлениях

Для каждого числа Nсуществует единственное представление (*), в к-ром 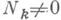и N_iN_i+1=0, i=0, 1, ..., k-1, число ненулевых коэффициентов в этом представлении равно w(N). Напр., 23=2⁴+2²+2¹+2⁰=2⁵-2³-2° и w(23) = 3. Так как p(N₁+N, N₂+N)=r(N₁, N₂ )для любых то ограничиваются рассмотрением кодов, не содержащих отрицательных чисел. Длиной кода Кназ. величина [log₂ В(К)]+1, где В(К)- наибольшее число кода К. Произвольному числу Вкода длины п однозначно соответствует слово b(B)-b_n-1...b₁b₀ в алфавите {0, 1} такое, что Если код исправляет tарифметич. ошибок, то код исправляет tошибок (типа замещения) в силу того, что 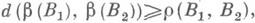где - метрика Хемминга (см. Код с исправлением ошибок). При исследовании задачи контроля сумматора обычно рассматривают кодирования 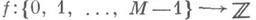(см. Кодирование и декодирование), обладающие свойством f(i+j)=f(i)+f(j) при i+j<M (что равносильно 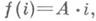где А=f(1)). В этом случае операция кодирования состоит в умножении кодируемого числа на А, а обнаружение ошибок в работе сумматора заключается в проверке делимости на Арезультата сложения. Код К _A,M= {0, A, ..., ( М-1)} наз. A-кодом мощности М. Расстояние A-кода равно минимальному w(Ai), i=l, ..., М-1. Напр., расстояние 3-кода произвольной мощности равно 2, код обнаруживает одиночные арифметич. ошибки и часто применяется в ЭВМ (в виде контроля по модулю 3). Наиболее исследованы (циклические и негациклические) А-коды мощности 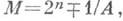характеризующиеся тем свойством, что вместе с числом b_i=0, 1, число В'=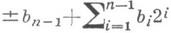 также принадлежит коду. Такие коды, называемые ( п, А) -к одами, удобно рассматривать как подмножества метрического пространства N_m= {0, 1, . .., т-1}, 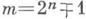с метрикой r _т (x, y)=w_m(x-y)=min{w(x-y), w(x-у-т)}. Расстояния (n, A )-кода в метриках р и р _т равны. С каждым (n, A )-кодом связан (n, A*)-код, где АА* = т, называемый двойственным. Если 2 или -2 -первообразный корень по модулю простого числа р, то ((р-1)/2, р)-код исправляет одиночные арифметич. ошибки и является совершенным в метрике r_m, т. е. метрические шары радиуса 1, описанные вокруг чисел кода, не только попарно не пересекаются, но и заполняют все N_m. В двойственном коде все расстояния между различными числами кода равны](р+1)/6[. Перечисленные результаты для кодов имеют аналоги в классе двоичных линейных циклических кодов, исправляющих ошибки. В то же время не известны арифметич. аналоги БЧХ-кодов, а также не известны верхние границы мощности кодов с заданными длиной и расстоянием, аналогичные границам для кодов, исправляющих ошибки. Еще большей спецификой обладают коды, исправляющие q-ичные (q>2) арифметич. ошибки. (q- ичной арифметической ошибкой наз. преобразование числа Nв число 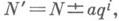а=1, ..., q-1; i=0, 1, ...), интерес к к-рым возрастает с развитием вычислительной техники. Так, в отличие от кодов, исправляющих ошибки при q=2^l (^l>1), не существует совершенных А-кодов, исправляющих одиночные q-ичные арифметич. ошибки, а при q=6 известны примеры таких кодов. Условия существования совершенных А-кодов имеют теоретико-числовой характер и связаны с изучением законов взаимности в числовых полях.

Лит.:[1] Дадаев Ю. Г., Арифметические коды, исправляющие ошибки, М., 1969; [2] Питерсон У., Уэлдон Э., Коды, исправляющие ошибки, пер. с англ., 2 изд., М., 1976; [3] Мasseу J. L., Garcia О. N., в кн.: Advances in Information Systems Science, v. 4, N. Y.-L., 1972, p. 273 - 326; [4] БояриновИ. М., Кабатянский Г. А., "Проблемы передачи информации", 1976, т. 12, в. 1, с. 16-23.

Г. А. Кабатянский.