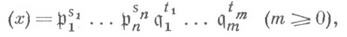КИТАЙСКАЯ ТЕОРЕМА ОБ ОСТАТКАХ
- КИТАЙСКАЯ ТЕОРЕМА ОБ ОСТАТКАХ
пусть А- ассоциативное и коммутативное кольцо с единицей и 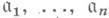 - такая совокупность идеалов кольца А, что
- такая совокупность идеалов кольца А, что 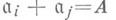 для любых тогда
для любых тогда 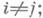 для любого набора элементов
для любого набора элементов  найдется элемент
найдется элемент 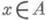 такой, что x=xi(mod a,), i=l, ..., п. В частном случае, когда А- кольцо целых чисел 2, К. т. об о. утверждает, что для любого набора попарно взаимно простых чисел а 1, ..., а п найдется целое число х, дающее заданные остатки при делении его на а 1,..., а п. В этой форме К. т. об о. была известна еще в Древнем Китае, с чем и связано название теоремы.
такой, что x=xi(mod a,), i=l, ..., п. В частном случае, когда А- кольцо целых чисел 2, К. т. об о. утверждает, что для любого набора попарно взаимно простых чисел а 1, ..., а п найдется целое число х, дающее заданные остатки при делении его на а 1,..., а п. В этой форме К. т. об о. была известна еще в Древнем Китае, с чем и связано название теоремы.
Наиболее часто К. т. об о. применяется в случае, когда А- дедекиндово кольцо и 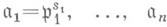 =
=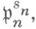 где
где  - различные простые идеалы в А(если идеалы a1, ..., а п удовлетворяют условию теоремы, то этим же свойством обладают и идеалы
- различные простые идеалы в А(если идеалы a1, ..., а п удовлетворяют условию теоремы, то этим же свойством обладают и идеалы  для любых натуральных s1, ..., sn). К. т. об о. в этом случае показывает, что для любого набора s1, ..., sn найдется
для любых натуральных s1, ..., sn). К. т. об о. в этом случае показывает, что для любого набора s1, ..., sn найдется  такой, что разложение главного идеала (х)в произведение простых идеалов имеет вид
такой, что разложение главного идеала (х)в произведение простых идеалов имеет вид
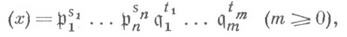
где идеалы p1,..., р п, q1,..., q т попарно различны (теорема о независимости показателей).
Лит.:[1] Кострикин А. И., Введение в алгебру, М., 1977; [2] Ленг С, Алгебра, пер. с англ., М., 1968; [3] его же, Алгебраические числа, пер. с англ., М., 1966.
Л. В. Кузьмин.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Полезное
Смотреть что такое "КИТАЙСКАЯ ТЕОРЕМА ОБ ОСТАТКАХ" в других словарях:
китайская теорема об остатках — КТО — [http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23] Тематики защита информации Синонимы КТО EN chinese remainder theoremCRT … Справочник технического переводчика
Китайская теорема об остатках — Несколько связанных утверждений известны под именем китайской теоремы об остатках. Эта теорема в её арифметической формулировке была описана в трактате китайского математика Сунь Цзы «Сунь Цзы Суань Цзин» (кит. упр. 孙子算经, пиньинь: sunzi suanjing) … Википедия
Сравнение по модулю — Сравнение[1] по модулю натурального числа n в теории чисел отношение эквивалентности на кольце целых чисел, связанное с делимостью на n. Факторкольцо по этому отношению называется кольцом вычетов. Совокупность соответствующих тождеств и… … Википедия
Система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия
Теория чисел — Теория чисел, или высшая арифметика раздел математики, изучающий целые числа и сходные объекты. В теории чисел в широком смысле рассматриваются как алгебраические, так и трансцендентные числа, а также функции различного происхождения, которые… … Википедия
Атака по времени — В криптографии атака по времени это атака по сторонним каналам, в которой атакующий пытается скомпрометировать криптосистему с помощью анализа времени, затрачиваемого на исполнение криптографических алгоритмов. Каждая логическая операция требует… … Википедия
Тест простоты — Тест простоты алгоритм, который по заданному натуральному числу определяет, простое ли это число. Различают детерминированные и вероятностные тесты. Определение простоты заданного числа в общем случае не такая уж тривиальная задача. Только… … Википедия
Алгоритм Фюрера — (англ. Fürer’s algorithm) быстрый метод умножения больших целых чисел. Алгоритм был построен в 2007 году швейцарским математиком Мартином Фюрером[1] из университета штата Пенсильвания как асимптотически более быстрый алгоритм, чем его… … Википедия
Криптосистема Рабина — – криптографический алгоритм с открытым ключом. Ее безопасность, как и у RSA, связана с трудностью разложения на множители. Безопасность схемы Рабина опирается на сложность поиска квадратных корней по модулю составного числа. Сложность этого… … Википедия
Сравнение по модулю натурального числа — В теории чисел сравнение[уточнить] по модулю натурального числа n задаваемое означенным числом отношение эквивалентности на множестве целых чисел, связанное с делимостью на него. Факторпространство по этому отношению называется «кольцом… … Википедия
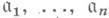 - такая совокупность идеалов кольца А, что
- такая совокупность идеалов кольца А, что 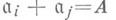 для любых тогда
для любых тогда 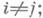 для любого набора элементов
для любого набора элементов  найдется элемент
найдется элемент 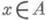 такой, что x=xi(mod a,), i=l, ..., п. В частном случае, когда А- кольцо целых чисел 2, К. т. об о. утверждает, что для любого набора попарно взаимно простых чисел а 1, ..., а п найдется целое число х, дающее заданные остатки при делении его на а 1,..., а п. В этой форме К. т. об о. была известна еще в Древнем Китае, с чем и связано название теоремы.
такой, что x=xi(mod a,), i=l, ..., п. В частном случае, когда А- кольцо целых чисел 2, К. т. об о. утверждает, что для любого набора попарно взаимно простых чисел а 1, ..., а п найдется целое число х, дающее заданные остатки при делении его на а 1,..., а п. В этой форме К. т. об о. была известна еще в Древнем Китае, с чем и связано название теоремы.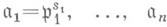 =
=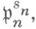 где
где  - различные простые идеалы в А(если идеалы a1, ..., а п удовлетворяют условию теоремы, то этим же свойством обладают и идеалы
- различные простые идеалы в А(если идеалы a1, ..., а п удовлетворяют условию теоремы, то этим же свойством обладают и идеалы  для любых натуральных s1, ..., sn). К. т. об о. в этом случае показывает, что для любого набора s1, ..., sn найдется
для любых натуральных s1, ..., sn). К. т. об о. в этом случае показывает, что для любого набора s1, ..., sn найдется  такой, что разложение главного идеала (х)в произведение простых идеалов имеет вид
такой, что разложение главного идеала (х)в произведение простых идеалов имеет вид