ИНВАРИАНТНОЕ ПОДПРОСТРАНСТВО
- ИНВАРИАНТНОЕ ПОДПРОСТРАНСТВО
допустимое подпространство, векторного пространства Vотносительно данного множества Млинейных отображений пространства Vв себя - подпространство U, удовлетворяющее условию  для всех
для всех 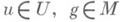 (иначе М-и нвариантное, М- допустимое подпространство).
(иначе М-и нвариантное, М- допустимое подпространство).
Ю. И. Мерзляков.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Смотреть что такое "ИНВАРИАНТНОЕ ПОДПРОСТРАНСТВО" в других словарях:
инвариантное подпространство — invariantinis poerdvis statusas T sritis fizika atitikmenys: angl. invariant subspace vok. invarianter Unterraum, m rus. инвариантное подпространство, n pranc. sous espace invariant, m … Fizikos terminų žodynas
Инвариантное подпространство — Подпространство линейного пространства называется инвариантным относительно оператора , действующего в пространстве , если для любого , иными словами, . Важными примерами инвариантны … Википедия
ИНВАРИАНТНОЕ ПОДПРОСТРАНСТВО — представления p группы (алгебры, кольца, полугруппы) Xв векторном пространстве (соответственно в топологич. векторном пространстве) Е векторное (соответственно замкнутое векторное) подпространство такое, что для любого и любоговыполняется… … Математическая энциклопедия
ПРЕДСТАВЛЕНИЕ ГРУППЫ — изображение элементов группы матрицами или преобразованиями линейного пространства, при к ром сохраняется исходная групповая структура. Поскольку достаточно хорошо изучены матричные группы, при исследовании произвольной группы стараются… … Физическая энциклопедия
Преобразования Лоренца — Преобразования Лоренца линейные (или аффинные) преобразования векторного (соответственно, аффинного) псевдоевклидова пространства, сохраняющее длины или, что эквивалентно, скалярное произведение векторов. Преобразования Лоренца… … Википедия
ВПОЛНЕ ПРИВОДИМАЯ МАТРИЧНАЯ ГРУППА — матричная группа Gнад произвольным фиксированным полем Р, все матрицы к рой одновременным сопряжением посредством нек рой матрицы над Рможно привести к клеточно диагональному виду, т. е. к виду где квадратные матрицы, а на остальных местах стоят… … Математическая энциклопедия
ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ — отображение векторного пространства в себя, при к ром образом суммы двух векторов является сумма их образов, а образом произведения вектора на число произведение образа вектора на это число. Если V векторное пространство, f заданное в нем Л. п. и … Математическая энциклопедия
РЕДУКТИВНОЕ ПРОСТРАНСТВО — такое однородное пространство G/Hсвязной группы Ли G, что в алгебре Ли группы G существует (H) инвариантное подпространство, дополнительное к подалгебре , являющейся алгеброй Ли группы H. Выполнение любого из следующих условий достаточно для того … Математическая энциклопедия
ЛИНЕЙНЫЙ ОПЕРАТОР — линейное преобразование, отображение между двумя векторными пространствами, согласованное с их линейными структурами. Точнее, отображение где Еи F векторные пространства над полем k, наз. л и н е й н ы м оператором из Ев F, если при всех… … Математическая энциклопедия
ЖОРДАНА РАЗЛОЖЕНИЕ — 1) Ж. р. функции ограниченной вариации представление функции f в виде где f1 и f2 монотонно возрастающие функции. Ж. р. наз. также представление обобщенной меры, или зарядаm(Е)измеримого множества Ев виде разности мер где хотя бы одна из мерm+… … Математическая энциклопедия
 для всех
для всех 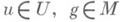 (иначе М-и нвариантное, М- допустимое подпространство).
(иначе М-и нвариантное, М- допустимое подпространство).