ДИХОТОМИЯ

- свойство линейной системы обыкновенных дифференциальных уравнений

с ограниченными непрерывными коэффициентами обладать такими положительными постоянными К, L,a, b что существует разложение Е ^п=Е ^т+Е ^п-т, для к-рого

(экспоненциальная Д.; при a=b=0 - обыкновенная Д.). Наличие экспоненциальной Д. эквивалентно тому, что неоднородная система

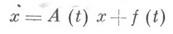
при любой ограниченной непрерывной функции f(t), имеет хотя бы одно ограниченное на решение (см. [1]). Теория Д. (см. [2]) перенесена на уравнения в банаховых пространствах, используется также для изучения потоков и каскадов на гладких многообразиях [4].

Лит.:[1] Рerron О., "Math. Z.", 1930, Bd 32, №-5, S. 703- 728; [2] Массера Х.-Л., Шеффер Х.-Х., Линейные дифференциальные уравнения и функциональные пространства, пер. с англ., М., 1970; [3] Далецкий Ю. Л., Крейн М. Г., Устойчивость решений дифференциальных уравнений в банаховом пространстве, М., 1970; [4] Аносов Д. В., "Тр. матем. ин-та АН СССР", 1967, т. 90.

Р. А. Прохорова.