ДИФФЁРЕНЦИРУЕМОСТЬ РЕШЕНИИ

дифференциальных уравнений- свойство решений дифференциальных уравнений, состоящее в существовании у решений определенного числа непрерывных производных по независимому переменному tи параметру m, входящему в уравнение. В теории дифференциальных уравнений вопрос ставится так: какими свойствами должна обладать правая часть уравнения, чтобы решение имело столько-то непрерывных производных по tи m? Вопрос о Д. р. наиболее систематически исследован для обыкновенных дифференциальных уравнений.

Пусть имеется уравнение вида (хможет быть также и вектором):

где ц. - параметр (тоже, вообще говоря, вектор), и пусть x(t, ц.) - его решение, определяемое начальным условием

Пусть рассматривается сначала Д. р. по t. В случае непрерывности fпо tи хв нек-рой области справедлива теорема существования непрерывного решения задачи (1) - (2), и тогда из тождества, получаемого после подстановки x(t,m) в (1), последует также существование непрерывной производной x't. Наличие пнепрерывных производных f по t и x обеспечивает существование п+1 непрерывных производных от решения по t; х _t⁽ⁿ⁾ можно найти (выразить через x(t,m))непоследовательным дифференцированием тождества, получаемого в результате подстановки x(t,m) в (1).

В ряде вопросов, напр, для построения асимптотики решения по параметру ц., необходимо исследовать производные по m от x(t,m). Для определенности рассмотрим задачу о существовании производных по m при m=0. Когда f(t, х,m) непрерывна и обладает непрерывными частными производными по хи m в нек-рой области, то h₁=x'_m существует и определяется из так наз. уравнения в вариациях (линейного относительно h₁), получаемого из (1), если обе части продифференцировать по h и положить h=0:

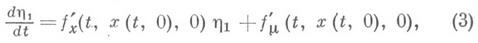
и при помощи начального условия

в случае, если х ₀ от h не зависит; если же х ₀=х ₀(h), то h₁|_t=t0= x₀(0).

Производная h_k от x(t,m) по m порядка к(при условии, что f обладает непрерывными частными производными до к-го порядка) определяется из уравнения в вариациях порядка k, к-рое отличается от (3) только неоднородностью, зависящей от t, x(t,0), h₁, ..., h_k-1. При наличии k+1 непрерывных производных от x(t,m) по m можно воспользоваться формулой Тейлора в качестве асимптотич. формулы для x(t,m) по m:

Это имеет важное значение, так как x(t,0) и h_i находятся из более простых уравнений, чем (1).

В случае аналитич. ависимости правой части от своих аргументов решение является аналитич. функцией параметра m (см., напр., [2]).

Вопрос о Д. р. по m сохраняет смысл также в ряде случаев, когда правая чаcть не является регулярно зависящей от m. Один из таких случаев имеет место, когда m входит множителем при производных:

Если (6) переписать в виде (1), т. е. разрешить относительно производных, то в правой части при m -> 0 появляется особенность типа полюса. Оказывается, что и в этом случае при наличии k+1 непрерывных производных от правых частей и при нек-рых специальных условиях, так наз. условиях устойчивости, справедливо разложение (5), где h_i- предельные значения производных по и. от решения (6) при определяемые из уравнений в вариациях, строящихся по тому же правилу: нужно продифференцировать (6) по m и положить m=0. Но при этом в отличие от регулярного случая система уравнений в вариациях будет более низкого порядка, чем (6), и начальные значения для h_i, несмотря на то, что у ₀, х ₀ от ц. не зависят, уже не будут нулевыми, а будут равны нек-рым, вообще говоря, отличным oт нуля, постоянным, получаемым по определенному правилу [3].

Лит.:[1] Петровский И. Г., Лекции по теории обыкновенных дифференциальных уравнений, 6 изд., М., 1970; [2] Тихонов А. Н., "Матем. сб.", 1948, т. 22, № 2, с. 193- 204; [3] Васильева А. Б., Бутузов В. Ф., Асимптотические разложения решений сингулярно возмущенных уравнений, М., 1973.

А. Б. Васильева.