- ДИФФЕРЕНЦИРОВАНИЕ ЧИСЛЕННОЕ
- нахождение производной функции численными методами. Д. ч. используется в случаях, когда методы дифференциального исчисления неприменимы (функция задана таблично), или их применение вызывает значительные трудности (функция имеет сложное аналитическое выражение).
Пусть на отрезке [ а, b]определена функция и=и (х)и заданы узловые точки х;, a=x1<x2< ...<xn=b. Совокупность точек ( х i, и i=и( х i)), i=l, ..., п, наз. таблицей. Результатом Д. ч. таблицы является функция
 в каком-либо смысле приближающая k-ю производную
в каком-либо смысле приближающая k-ю производную  функции на нек-ром множестве
функции на нек-ром множестве  точек х. Применение Д. ч. целесообразно, когда получение функции
точек х. Применение Д. ч. целесообразно, когда получение функции  для каждого
для каждого  требует незначительной затраты вычислительных средств. Обычно используются линейные методы Д. ч., где результат Д. ч. записывается в виде
требует незначительной затраты вычислительных средств. Обычно используются линейные методы Д. ч., где результат Д. ч. записывается в виде
 - функции, определенные на
- функции, определенные на  Наиболее распространенный метод получения формул (1) состоит в следующем: строят функцию
Наиболее распространенный метод получения формул (1) состоит в следующем: строят функцию 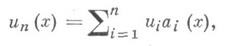
интерполирующую и(х), и полагают

Точность алгоритмов, основанных на интерполяционных формулах Лагранжа, Ньютона и др., существенным образом определяется выбором способа интерполяции и может быть иногда весьма низкой даже для достаточно гладких функций и=и (х)и при большом числе узловых точек (см. [1]). От этого недостатка часто свободны алгоритмы Д. ч., использующие сплайн-интерполяцию (см. [2]). Если требуется вычисление приближенных значений производной только в узловых точках х i, то формула (1) принимает вид

и
 полностью определяется заданием для данного kматрицы коэффициентов
полностью определяется заданием для данного kматрицы коэффициентов  Формулы типа (2) наз. разностными формулами Д. ч. Коэффициенты akij этих формул определяют из условия наивысшего порядка малости по
Формулы типа (2) наз. разностными формулами Д. ч. Коэффициенты akij этих формул определяют из условия наивысшего порядка малости по 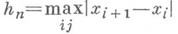 разности
разности
Формулы (2), как правило, весьма просты и удобны на практике. Напр., при h=hn=(x2-x1)=(x3 -х 2)= ... =( х п- х п-1) они имеют вид:
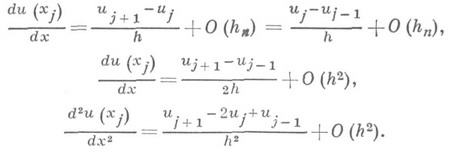
Алгоритмы Д. ч. часто применяются к таким таблицам, в к-рых значения и( х i )заданы (или получены) неточно. В этом случае требуется их предварительное сглаживание, так как непосредственное применение Д. ч. может привести к большим погрешностям в результатах (см. [3]).
Лит.:[1] Березин И. С., Жидков Н. П., Методы вычислений, 3 изд., т. 1, М., 1966; [2] Альберг Дж., Нильсон Э., Уолш Дж., Теория сплайнов и ее приложения, пер. с англ., М., 1972; [3] Морозов В. А., в кн.: Вычислительные методы и программирование, в. 14, М., 1970, с. 46-62.
Л. А. Морозов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
