АЛГОРИТМОВ СОЧЕТАНИЯ

название, установившееся за рядом конкретных способов конструирования новых алгоритмов из нескольких заданных.

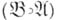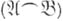В применении к нормальным алгорифмам наибольшую известность получили следующие А. с.: нормальная композиция двух нормальных алгорифмов .нормальное объединение двух нормальных алгорифмов 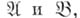нормальное разветвление двух нормальных алгорифмов управляемое нормальным алгорифмом нормальное повторение 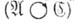нормального алгорифма , управляемое нормальным алгорифмом . Если 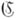- нормальные алгорифмы в нек-ром алфавите А, то упомянутые их сочетания являются нормальными алгорифмами в нек-ром фиксированном расширении Аи удовлетворяют следующим условиям: а) для любого слова 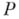в имеет место (теорема композиции); б) для любого слова Рв Аимеет место (теорема объединения); в) для любого слова Рв А

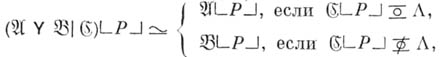
причем если ( определено, то определено и 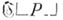(теорема разветвления); г) для любых слов и 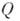в A графическое равенство имеет место тогда и только тогда, когда может быть указан ряд слов 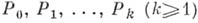в алфавите 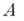таких, что

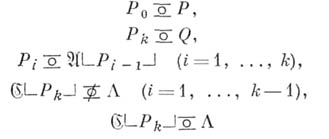
(теорема повторения). Аналогичные теоремы могут быть получены и для Тьюринга машин. В теории рекурсивных функций наибольшее употребление нашли их сочетания, доставляемые оператором подстановки, оператором примитивной рекурсии и m-оператором.

Теоремы об А. с. вскрывают весьма существенную особенность осуществленных стандартизации общего понятия алгоритма - их "устойчивость" по отношению к естественным способам А. с. Это обстоятельство является одним из наиболее веских доводов в пользу основной гипотезы теории алгоритмов ( Чёрча тезиса). Теоремы об А. с. составляют важный раздел общей теории алгоритмов. Будучи доказаны однажды, они позволяют в дальнейшем убеждаться в осуществимости сложных и громоздких алгоритмов без фактического выписывания определяющих их схем.

Значительный интерес для общей теории алгоритмов представляет вопрос о разыскании базиса, позволяющего при фиксированном наборе способов А.- с. порождать любой алгоритм к.-л. интересующего нас класса.

Лит.:[1] Марков А. А., Теория алгорифмов, "Тр. Матем. ин-та АН СССР", 1954, т. 42, с. 94-145; [2] Клини С. К., Введение в метаматематику, пер. с англ., М., 1957; [3] Успенский В. А., Лекции о вычислимых функциях, М., 1960; [4] Мальцев А. И., Алгоритмы и рекурсивные функции, М., 1965. Н. М. Нагорный.