ДИВИЗОРИАЛЬНЫЙ ИДЕАЛ

- дробный идеал а целостного коммутативного кольца Атакой, что а=А:(А: а )(здесь А: а обозначает множество элементов хиз поля частных кольца А, для к-рых ). Иногда Д. и. наз. дивизором кольца. Для любого дробного идеала идеал дивизориален. Множество D(А)Д. и. кольца Аявляется решеточно упорядоченным коммутативным моноидом (полугруппой), если произведением двух Д. и. а и bсчитать 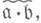а положительными (или эффективными) считать целые Д. и. 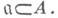Моноид D(A)является группой тогда и только тогда, когда кольцо Авполне целозамкнуто; при этом обратным к дивизору а будет А: а.

Обычно Д. и. рассматривают в кольце Крулля (напр., в нётеровом целозамкнутом кольце); в этом случае простые идеалы высоты 1 дивизориальны и образуют базис абелевой группы дивизоров D(A). Этот результат, по существу, был установлен Э. Артином (Е. Artin) и Б. Л. Ван дер Варденом (В. L. Van der Waerden) (см. [1]) в их теории квазиравенства идеалов (идеалы а и bквазиравны, если и завершил одну из центральных тем алгебры того времени - изучение разложения идеалов.

Главные дробные идеалы, а также обратимые дробные идеалы являются дивизориальными и образуют соответственно подгруппы F(A)и J(А)в D(A). Фактор-группы D(A)lF{A) = C{A )и J(A)/F(A) = Pic(A)наз. соответственно классов дивизоров группой и Динара группой кольца А.

Лит.:[1] Ван дер Варден Б. Л., Алгебра, пер. с рем., М., 1976; [2] Бурбаки Н., Коммутативная алгебра, пер. с франц., М., 1971.

В. И. Данилов.