- ДИАГОНАЛЬНАЯ ЦЕПНАЯ ДРОБЬ
- цепная дробь

у к-рой последовательности
 и
и  должны удовлетворять следующим условиям:
должны удовлетворять следующим условиям:1) числа а п и b п целые; |b п| = 1;
 если
если  aw
aw 2, если 0<w<
2, если 0<w< ;
;2)
 для всех га; если
для всех га; если  то
то  для бесконечного множества и;
для бесконечного множества и;3) Qn<Qn+1 для всех n;
4) все подходящие дроби цепной дроби суть все несократимые дроби
 такие, что
такие, что 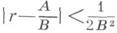 и B>0, где r - значение цепной дроби.
и B>0, где r - значение цепной дроби.Для каждого действительного числа r существует одна и только одна Д. ц. д., значение к-рой равно r;эта дробь периодична, если r- квадратическая иррациональность.
В. И. Нечаев
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
