- ГРУДЫ И ПОЛУГРУДЫ
- алгебры с одной тернарной операцией, удовлетворяющей нек-рым тождествам. Груды (г.) определяются тождествами:

а полугруды (п.) - тождествами:

Всякая груда является полугрудой.
Если в множестве Ф (А, В).всех взаимно однозначных отображений множества Ана множество Вопределить тернарную операцию, ставя в соответствие упорядоченной тройке отображений
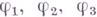 отображение, являющееся суперпозицией
отображение, являющееся суперпозицией  то
то  становится г. Любая г. изоморфна нек-рой г. взаимно однозначных отображений. Если в произвольной группе Gввести тернарную операцию, полагая
становится г. Любая г. изоморфна нек-рой г. взаимно однозначных отображений. Если в произвольной группе Gввести тернарную операцию, полагая  то также получится г. (груда, ассоциированная с данной группой). Понятие г. было введено при рассмотрении вышеуказанной тернарной операции в абелевой группе (см. [1]). Г. изучались и с абстрактной точки зрения (см. [2], [3]). В частности, Р. Бэр доказал [2], что если в г. Sфиксировать произвольный элемент
то также получится г. (груда, ассоциированная с данной группой). Понятие г. было введено при рассмотрении вышеуказанной тернарной операции в абелевой группе (см. [1]). Г. изучались и с абстрактной точки зрения (см. [2], [3]). В частности, Р. Бэр доказал [2], что если в г. Sфиксировать произвольный элемент 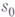 , то операции, определяемые равенствами
, то операции, определяемые равенствами 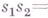
 задают на Sструктуру группы, в к-рой s0 является единицей; при этом г., ассоциированная с этой группой, совпадает с исходной г., а группы, получаемые из данной г. фиксированием различных ее элементов, изоморфны. Другими словами, многообразие всех г. эквивалентно многообразию всех групп.
задают на Sструктуру группы, в к-рой s0 является единицей; при этом г., ассоциированная с этой группой, совпадает с исходной г., а группы, получаемые из данной г. фиксированием различных ее элементов, изоморфны. Другими словами, многообразие всех г. эквивалентно многообразию всех групп.
Совокупность
 всех бинарных отношений между элементами множеств Аи Вявляется п. относительно тройного умножения:
всех бинарных отношений между элементами множеств Аи Вявляется п. относительно тройного умножения: 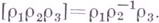 Множество всех обратимых частичных отображений Ав В также замкнуто относительно тройного умножения и является обобщенной грудой (см. [4]), то есть п. с тождествами:
Множество всех обратимых частичных отображений Ав В также замкнуто относительно тройного умножения и является обобщенной грудой (см. [4]), то есть п. с тождествами:

Обобщенные г. находят приложение в основаниях дифференциальной геометрии при рассмотрении координатных атласов (см. [5]).
П. тесно связаны с полугруппами с инволюцией. Если на полугруппе Sзадана инволюция q, являющаяся антиавтоморфизмом, то тернарная операция [s1s2s3]=s1q(s2)s3 превращает S в п. Всякая п. изоморфна подполугруде нек-рой полугруппы с инволюцией (см. [4]).
Лит.: [1]
 Н., "Math. Z.", 1924, Bd 20, S. 165-87; [2] BaerR., ".Т. reine und angew. Math.", 1929, Bd 160, S. 199-207; [3] Сertaine J., "Bull. Amer. Math. Soc.", 1943, v. 49, p. 869-77; [4] Вагнер В. В., "Матем. сб.", 1953, т. 32, № 3, с. 545-632; [5] его же, Основания дифференциальной геометрии и современная алгебра, в кн.: Тр. 4 Всесоюзного матем. съезда, т. 1, Л., 1963, с. 17-29; [6] Глускин Л. М., в сб.: Теория полугрупп и ее приложения, т. 1, Саратов, 1965, с. 179-97. 198-228. В. Н. Салий.
Н., "Math. Z.", 1924, Bd 20, S. 165-87; [2] BaerR., ".Т. reine und angew. Math.", 1929, Bd 160, S. 199-207; [3] Сertaine J., "Bull. Amer. Math. Soc.", 1943, v. 49, p. 869-77; [4] Вагнер В. В., "Матем. сб.", 1953, т. 32, № 3, с. 545-632; [5] его же, Основания дифференциальной геометрии и современная алгебра, в кн.: Тр. 4 Всесоюзного матем. съезда, т. 1, Л., 1963, с. 17-29; [6] Глускин Л. М., в сб.: Теория полугрупп и ее приложения, т. 1, Саратов, 1965, с. 179-97. 198-228. В. Н. Салий.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
