НЕЕВКЛИДОВА ГЕОМЕТРИЯ

геометрия, сходная с геометрией Евклида в том, что в ней определено движение фигур, но отличающаяся от евклидовой геометрии тем, что один из пяти ее постулатов (второй или пятый) заменен его отрицанием. Отрицание одного из евклидовых постулатов (1825) явилось значительным событием в истории мысли, ибо послужило первым шагом на пути к теории относительности. Второй постулат Евклида утверждает, что любой отрезок прямой можно неограниченно продолжить. Евклид, по-видимому, считал, что этот постулат содержит в себе и утверждение, что прямая имеет бесконечную длину. Однако в "эллиптической" геометрии любая прямая конечна и, подобно окружности, замкнута. Пятый постулат утверждает, что если прямая пересекает две данные прямые так, что два внутренних угла по одну сторону от нее в сумме меньше двух прямых углов, то эти две прямые, если продолжить их неограниченно, пересекутся с той стороны, где сумма этих углов меньше суммы двух прямых. Но в "гиперболической" геометрии может существовать прямая CB (рис. 1), перпендикулярная в точке С к заданной прямой r и пересекающая другую прямую s под острым углом в точке B, но, тем не менее бесконечные прямые r и s никогда не пересекутся.

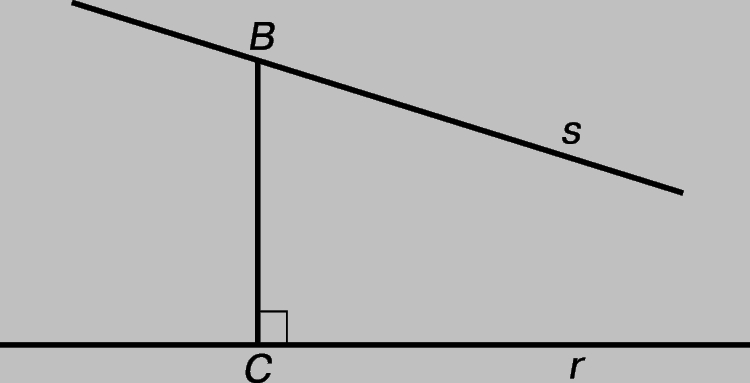
Рис. 1. В ГИПЕРБОЛИЧЕСКОЙ ГЕОМЕТРИИ может существовать прямая CB, перпендикулярная данной прямой r и пересекающая другую данную прямую s под острым углом в точке B так, что бесконечный луч s не пересекает прямую r.

Из этих пересмотренных постулатов следовало, что сумма углов треугольника, равная 180° в евклидовой геометрии, больше 180° в эллиптической геометрии и меньше 180° в гиперболической геометрии.
История. Первым неевклидовым геометром, вероятно, можно считать самого Евклида. Его нежелание использовать "несамоочевидный" пятый постулат следует хотя бы из того, что свои первые двадцать восемь предложений Евклид доказывает, не прибегая к этому постулату. С первого века до н.э. до 1820 математики пытались вывести пятый постулат из остальных, но преуспели лишь в замене его различными эквивалентными допущениями, такими, как "две параллельные линии всюду равно удалены друг от друга" или "любые три точки, не расположенные на одной прямой, принадлежат окружности". Ближе всех подошел к цели иезуит, логик и математик Дж.Саккери (1667-1733), который начал свои исследования с так называемого четырехугольника Саккери (рис. 2), т.е. с четырехугольника BCED, у которого BC = DE, а углы при вершинах C и E прямые. Заметив, что углы при вершинах B и D обязательно равны, Саккери рассмотрел поочередно три гипотезы: верхние углы четырехугольника тупые, прямые и острые. Он доказал, что любая из этих гипотез, если ее принять для какого-нибудь одного такого четырехугольника, остается в силе для всех таких четырехугольников. Саккери намеревался обосновать гипотезу о том, что верхние углы прямые, доказав, что любая другая гипотеза приводит к противоречию. Вскоре он отверг гипотезу о тупом угле (и тем самым лишил себя возможности открыть эллиптическую геометрию), поскольку, как и все геометры до 1854, рассматривал второй постулат как утверждение о том, что прямая имеет бесконечную длину, и отказываться от этого постулата он не хотел. Точно также Саккери в конце концов отверг и гипотезу об остром угле, но прежде, чем принять это ошибочное решение, он, сам того не ведая, открыл многие теоремы геометрии, получившей впоследствии название гиперболической.

Рис. 2. ЧЕТЫРЕХУГОЛЬНИК САККЕРИ - четырехугольник BCED с BC = ED и прямыми углами при вершинах C и E. Евклидова геометрия требует, чтобы углы B и D также были прямыми. В эллиптической геометрии эти углы - тупые, а в гиперболической - острые.

К. Гаусса (1777-1855) принято считать одним из величайших математиков всех времен. Он первым подошел к проблеме с современной точки зрения, согласно которой геометрию, отрицающую пятый постулат, надлежит развивать ради нее самой, не ожидая, что при этом возникнет какое-то противоречие. Письма Гаусса к друзьям говорят о том, что к 1816 он преодолел традиционный предрассудок относительно неизбежности противоречия и развил "антиевклидову" геометрию, удовлетворяющую гипотезе Саккери об остром угле. Но, опасаясь насмешек, он воздерживался от публикации этих идей и тем самым позволил разделить честь открытия гиперболической геометрии (примерно в 1825) венгру Я. Бойяи (1802-1860) и русскому Н. И. Лобачевскому (1793-1856). Бойяи опубликовал свою работу до того, как услышал о Лобачевском, а последний, судя по всему, так никогда и не узнал об исследованиях Бойяи. В 1854 Б. Риман (1826-1866) заметил, что из неограниченности пространства еще не следует его бесконечная протяженность. Смысл этого утверждения станет яснее, если представить, что в неограниченной, но конечной вселенной астроном в принципе мог бы увидеть в телескоп, обладающий достаточно высокой разрешающей способностью, свой собственный затылок (если отвлечься от небольшой детали, связанной с тем, что свет, отраженный от затылка, достиг бы глаза астронома через тысячи миллионов лет). В своем доказательстве того, что внешний угол при любой вершине треугольника больше внутреннего угла при любой из двух остальных вершин, Евклид неявно использовал бесконечную длину прямой. Из этой теоремы тотчас же следует теорема о том, что сумма любых двух углов треугольника меньше суммы двух прямых углов. Если отказаться от бесконечной длины прямой, то гипотеза Саккери о тупом угле становиться верной и из нее следует, что сумма углов треугольника больше суммы двух прямых. Такое положение дел было давно известно в сферической тригонометрии, где стороны треугольника являются дугами больших кругов. Риман внес эпохальный вклад, распространив представление о конечном, но неограниченном пространстве с двух на три и большее число измерений.
Эллиптическая плоскость. Ф. Клейн (1849-1925) первым увидел, как избавить сферическую геометрию от одного из ее недостатков - того, что две лежащие в одной плоскости "прямые" (два больших круга на сфере) имеют не одну общую точку, а две (рис. 3,а). Так как для каждой точки существует одна-единственная точка-антипод (диаметрально противоположная точка), а для любой фигуры существует ее дубликат из точек-антиподов, мы можем, ничем не жертвуя, но многое приобретая, абстрактно отождествить обе точки такой пары, объединив их в одну. Таким образом можно изменить смысл термина "точка", условившись впредь называть "одной точкой" пару диаметрально противоположных точек. Иначе говоря, точки так называемой "эллиптической" плоскости представлены на единичной сфере парами точек-антиподов или диаметрами, соединяющими точки-антиподы. Вся эллиптическая прямая замкнута, как окружность, но, поскольку каждая из ее точек представлена двумя точками-антиподами на единичной сфере, полная длина эллиптической прямой равна половине длины окружности большого круга, т.е. ее полная длина равна p.

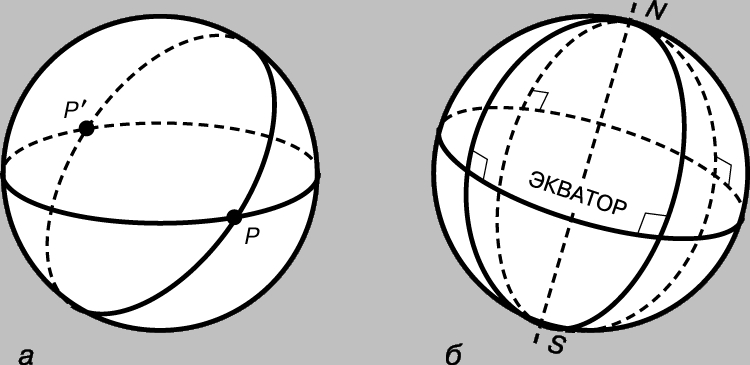
Рис. 3. а - на эллиптической плоскости "точка" представлена двумя точками-антиподами на сфере, например, точками P и P'. б - диаметр, соединяющий северный и южный полюсы сферы, на эллиптической плоскости является "полюсом" экватора.

Такое представление с помощью диаметров и диаметральных плоскостей сферы (при котором диаметр, соединяющий северный и южный полюсы сферы, является "полюсом" экватора), показывает, что все свойства действительной проективной плоскости сохраняются и для эллиптической плоскости.
Геометрия порядка. Один из подходов к построению гиперболической геометрии исходит из некоторых фундаментальных аксиом порядка, справедливых и в евклидовой, но не в эллиптической геометрии. Если считать "точки" исходными понятиями, то запись [[ABC]] означает, что точка B лежит "между" точками A и C (это первичное отношение мы принимаем, не пытаясь его определить). Первые четыре аксиомы порядка утверждают, что 1) существует по крайней мере две точки; 2) если A и B - две различные точки, то существует по крайней мере одна точка C, для которой [[ABC]]; 3) эта точка C отлична от точки A и 4) порядок [[ABC]] влечет за собой [[CBA]], но не [[BCA]]. "Отрезок" AB, по определению, состоит из точек P, для которых [[APB]], а "луч" A/B ("исходящий из A в другую сторону, чем B") - из точек Q, для которых [[QAB]]. "Прямая" AB состоит из отрезка AB, точек A, B и двух лучей A/B, B/A. Пятая аксиома утверждает, что если C и D - различные точки на прямой AB, то A лежит на прямой CD (из этой же аксиомы следует, что прямые AB и CD совпадают). Шестая аксиома дает нам точку вне данной прямой, а седьмая, сформулированная М. Пашем (1843-1931), позволяет определить плоскость как множество всех точек, коллинеарных с парами точек на одной или двух сторонах данного треугольника.
Абсолютная геометрия. Большая часть вклада Бойяи связана с теми разделами гиперболической геометрии, которые принадлежат и евклидовой геометрии. Его "абсолютная геометрия" может быть выведена из геометрии порядка, если к последней добавить еще одно фундаментальное отношение, а именно "конгруэнтность". Это отношение определяется пятью аксиомами типа "Если ABC и A'B'C' - два треугольника, таких, что BC є B'C', CA є C'A', AB є A'B', а D и D' - еще две точки, такие, что [[BCD]] и [[B'C'D']] и BD є B'D', то AD є A'D'". Эти аксиомы служат основой теории длины и позволяют распространить отношение конгруэнтности с пар точек на углы. Определив обычным образом окружность, мы можем рассматривать первые четыре постулата Евклида как теоремы и доказать его первые двадцать восемь предложений, заменив слово "параллельные" на "не пересекающиеся". Однако необходимо тщательно избегать любого обращения к нашему обычному представлению о сумме углов треугольника; например, мы не можем более утверждать, что углы, опирающиеся на один и тот же сегмент окружности, равны, так как доказательство этого предложения зависело бы от суммы углов треугольника. С другой стороны, мы можем доказать, что три высоты остроугольного треугольника пересекаются в одной точке, построить теорию правильных многоугольников и правильных многогранников (с небольшими оговорками). Уточнив понятие параллельности (определив как параллельные лучи, которые просто не пересекаются), мы можем показать, что параллельность - отношение симметричное и транзитивное (т. е. если прямая r параллельна прямой s, то s параллельна r; если r параллельна s, а s параллельна t, то r параллельна t). Множество прямых, параллельных данному лучу, называется "пучком параллельных"; он содержит единственную прямую, проходящую через любую заданную точку. Следуя аналогии с обычным пучком (состоящим из всех прямых, проходящих через точку), мы можем считать, что пучок параллельных определяет "бесконечно удаленную точку", или, по терминологии Д. Гильберта (1862-1943), "конец". Вместо того, чтобы говорить, что два луча (или две прямые) параллельны или что они принадлежат некоторому пучку параллельных M, мы говорим, что два луча имеют общий конец M. Луч, проходящий через точку C и принадлежащий данному пучку параллельных, принято обозначать CM, как если бы это был отрезок; тот же символ CM можно использовать и для обозначения всей прямой. Если BM и CM - параллельные лучи, то фигура MCB называется "асимптотическим треугольником", поскольку она во многом ведет себя, как обычный треугольник. В частности, два асимптотических треугольника конгруэнтны, если у них имеется по конгруэнтной стороне и конгруэнтному углу.
Гиперболическая плоскость. Из абсолютной геометрии Бойяи можно вывести евклидову геометрию, добавив евклидову (или аффинную) аксиому: через точку B, не лежащую на данной прямой r, можно провести не более одной прямой, параллельной данной. Гиперболическую геометрию можно вывести из абсолютной геометрии, добавив гиперболическую аксиому, повторяющую только что приведенную, но без отрицания "не" во втором случае. Таким образом, лучи BM и BN на рис. 4 могут быть оба параллельны r, а если M и N их концы, то r называется "прямой MN". Любая прямая, например t, являющаяся продолжением стороны угла РNBM, образует с r пару "гиперпараллельных", т.е. пару прямых, которые не пересекаются и не параллельны. Две такие прямые имеют единственный общий перпендикуляр. Множество прямых, перпендикулярных данной прямой a, называются "пучком гиперпараллельных" с "осью" a.

Рис. 4. ЛЮБАЯ ПОЛУПРЯМАЯ, например t, являющаяся продолжением стороны угла NBM, образует с r пару "гиперпараллельных", т.е. две прямые, которые не пересекаются и не параллельны.

Отражение относительно BC показывает, что РCBM и РNBC - равные острые углы. Лобачевский назвал каждый из них "углом параллельности" П(a), где a - длина BC. Он показал, что функция П(a) монотонно убывает от p ¤ 2 до 0, когда a возрастает от 0 до беск. Треугольник BMN естественно назвать "дважды асимптотическим треугольником". Два дважды асимптотических треугольника конгруэнтны, если имеют конгруэнтные углы. Если отрезок CB возрастает до тех пор, пока не превратится в луч CL, то BMN превращается в "трижды асимптотический треугольник" LMN, все три вершины которого являются концами (все три стороны такого треугольника бесконечны, а все три угла равны нулю). Все трижды асимптотические треугольники конгруэнтны. Одной из самых прекрасных страниц в литературе по неевклидовой геометрии со времен Лобачевского считается предложенное Г.Либманом доказательство того, что площадь треугольника остается конечной, когда две (или три) его стороны становятся бесконечными. Доказательство сводится к разбиению асимптотического треугольника на бесконечную последовательность конечных треугольников и перекладыванию их с соблюдением одного условия: все они должны умещаться внутри некоторого конечного пятиугольника. Метод Либмана восполняет один из двух недостающих шагов в предложенном Гауссом красивом доказательстве того, что площадь любого треугольника пропорциональна его "угловому дефекту" - величине, показывающей, насколько сумма углов треугольника меньше двух прямых. Аналогия с выражением (A + B + C) - p для площади сферического треугольника (на единичной сфере) наводит на мысль о естественной единице измерения, при которой площадь треугольника ABC просто равна p - (A + B + C). Используя эту единицу, Лобачевский выразил угол параллельности, соответствующий расстоянию x, формулой П(x) = 2arctg e-x.
Кривые, ортогональные обычному пучку прямых, имеют вид концентрических окружностей; кривые, ортогональные пучку параллельных, имеют вид концентрических "орициклов". В действительности орицикл - это предельная форма окружности, центр которой уходит в бесконечность (так, что диаметры окружности становятся параллельными).
Евклидовы модели неевклидовых геометрий. Ф. Вахтер (1792-1817) за несколько месяцев до безвременной кончины сообщил в письме к Гауссу о своем наблюдении: если пятый постулат Евклида ложен, то сфера, радиус которой стремиться к бесконечности, приближается к предельной поверхности, чья внутренняя геометрия совпадает с геометрией евклидовой плоскости. Тем самым Вахтер предвосхитил появление "орисферы", сыгравшей важную роль в работах Бойяи и Лобачевского. Эта поверхность получается при вращении орицикла вокруг любого из его диаметров. Кривые на орисфере, которые ведут себя, как евклидовы прямые, - орициклы, по которым орисферу пересекают ее диаметральные плоскости. А. Пуанкаре (1854-1912) открыл представление гиперболического пространства с помощью конформной модели, в которой геометрическое место концов имеет вид плоскости W в евклидовом пространстве, а сферам с центрами в W соответствуют плоскости гиперболического пространства. Заменив сферы полусферами, Пуанкаре получил возможность представить все гиперболическое пространство с помощью половины евклидова пространства, а именно всеми точками, лежащими по одну сторону от W. Один пучок концентрических орисфер представлен плоскостями, параллельными W; можно доказать, что евклидовы расстояния в такой плоскости пропорциональны соответствующим геодезическим на орисфере, что полностью согласуется с наблюдением Вахтера. Рассматривая сечение трехмерной модели Пуанкаре плоскостью, перпендикулярной W, мы получим модель аналогичную модели Пуанкаре для гиперболической плоскости. В этой модели геометрическое место концов имеет вид евклидовой прямой. В другой модели геометрическое место концов имеет вид окружности w, а прямые на гиперболической плоскости - дуг окружностей, ортогональных w. Две параллельные дуге r, проходящие через точку B, - просто дуги, проходящие через точку B и касающиеся дуги r в ее концах, как на рис. 5.

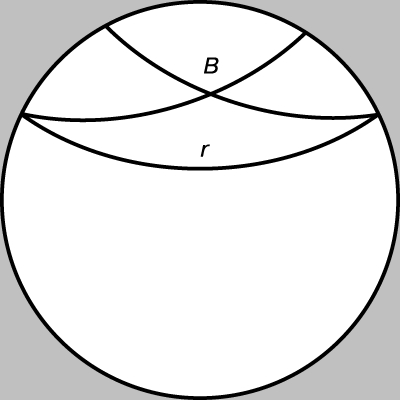
Рис. 5. ПАРАЛЛЕЛЬНЫЕ BC и BD к r, проходящие через точку B, - это просто две дуги, проходящие через точку B так, что они касаются r в ее концах. Эта модель "конформна", так как углы сохраняются, хотя расстояния неизбежно искажаются.

Такая модель называется "конформной" потому, что углы сохраняют свою величину, хотя расстояния неизбежно искажаются. Если пойти на искажение углов, то дуги можно заменить хордами, как на рис. 6. Эту более простую модель предложил в 1868 году Э. Бельтрами (1835-1900) для доказательства того, что гиперболическая геометрия так же логически непротиворечива, как и евклидова (хотя и Бойяи и Лобачевский были интуитивно убеждены, что их исследования никогда не приведут к двум противоречащим друг другу утверждениям, ни один из них не дожил до строгого доказательства непротиворечивости гиперболической геометрии). В модели Бельтрами множество прямых, проходящих через точку A, представлено обычным пучком параллельных или гиперпараллельных в зависимости от того, находится ли A внутри w, на w или вне w. В последнем случае (см. нижнюю часть рис. 6) ось пучка гиперпараллельных есть "поляра" точки A, соединяющая точки касания двух касательных, проведенных из точки A. Иначе говоря, две перпендикулярные прямые гиперболической плоскости представлены двумя прямыми, "сопряженными" относительно w. Такого рода идеи относятся к проективной геометрии; действительно, w можно рассматривать как коническое сечение на действительной проективной плоскости; в этом случае мы приходим к модели А.Кэли (1821-1895) и Ф. Клейна. Это коническое сечение w, геометрическое место концов, есть то, что Кэли назвал "абсолютом". (Преисполненный энтузиазмом, он сначала даже писал это слово с прописной буквы "А", но позднее перешел на строчную "а" во избежание упрека в непочтительности). Чтобы быть совершенно точным, следует отметить, что проективная плоскость, на которой работал Кэли, была не действительной, а комплексной: Кэли разрешал w быть коническим сечением, не содержащим действительных точек, отчего геометрия становится не гиперболической, а эллиптической.

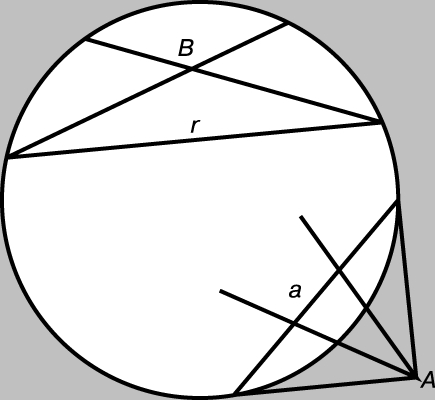
Рис. 6. В ЭТОЙ КОНФОРМНОЙ МОДЕЛИ, если мы согласимся, что углы также искажаются, дуги, изображенные на рис. 5, можно заменить их хордами. В нижней части рисунка ось пучка параллельных - "поляра" точки A, соединяющая точки касания двух касательных, проведенных из A.