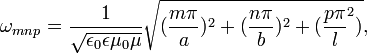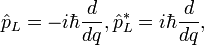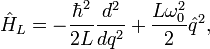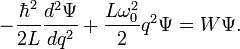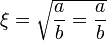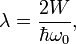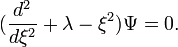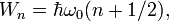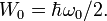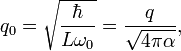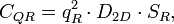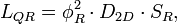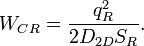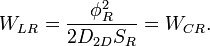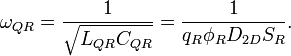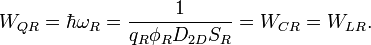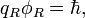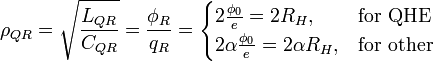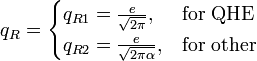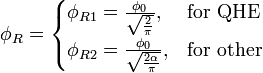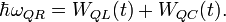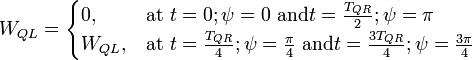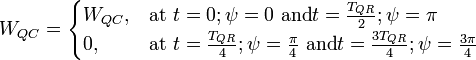Квантовый электромагнитный резонатор

Квантовый электромагнитный резонатор (КвЭР) (Quantum Electromagnetic Resonator) – замкнутой топологический объект в трехмерном пространстве, в общем случае ‘’полость’’ произвольной формы, которая имеет определенную ‘’поверхность’’ с определенной ‘’толщиной’’. В противоположность классическому случаю, в ней отсутствуют ‘’электромагнитные волны’’ и потери на излучение, но имеют место “нескончаемые” колебания фазово смещенного электромагнитного поля, которые вытекают из квантовых свойств КвЭР.

История вопроса

Так сложилось исторически, что физические реактивные величины такие, как емкость и индуктивность практически не рассматривались не только в квантовой, но даже и в классической теоретической электродинамике. Дело в том, что последние не входят в явном виде в систему уравнений Максвелла, в результате решения которой всегда получались электромагнитные поля, и если иногда в получаемых решениях и возникали размерные коэффициенты, которые можно было связать с емкостью или индуктивностью, то и отношение к ним было соответствующее. Не менее известно также, что «полевой подход» приводит к появлению «дурных бесконечностей», обусловленных рассмотрением движения «математической точки» (с электрическим зарядом) под воздействием силовых полей. Не избежала «дурных бесконечностей» и общепризнанная квантовая электродинамика, в рамках которой были также разработаны мощные методы «компенсации дурных бесконечностей».

Напротив, в прикладной физике понятие емкости и индуктивности нашло широкое применение, сначала в электротехнике, а потом в радиоэлектронике. Основным результатом применения реактивных параметров в прикладной физике является сегодня широкое распространение информационных технологий, которые базируются на генерации, приеме и передаче электромагнитных волн на различной частоте. В тоже время неразработанность на теоретическом уровне физических понятий для емкости и индуктивности сегодня уже становится в определенной мере сдерживающим фактором в развитии информационных технологий вообще и квантового компьютинга в частности. Достаточно вспомнить, что квантовое рассмотрение классического механического осциллятора было реализовано в эпоху создания квантовой механики (как одна из иллюстраций ее практического применения), тогда как квантовое рассмотрение 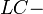$LC - \$ контура было теоретически поставлено только в начале 70-х годов 20-го века а детальное рассмотрение началось только в средине 90-х годов.

Впервые необходимость решения уравнения Шредингера для квантового 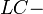$LC - \$ контура была поставлена в монографии Луизелла (1973) ^[1]. Поскольку тогда еще не было понимания, что собой представляют квантовые реактивные параметры (да и практических примеров тогда не было), то поэтому широкого распространения данный подход не получил. Теоретически корректное введение квантовой емкости, которое базировалось на плотности состояний впервые введено Лурием (1988) ^[2] при рассмотрении квантового эффекта Холла (КЭХ). К сожалению тогда не были введены квантовые индуктивности, которые также вытекали из плотности состояний, и поэтому полноценного рассмотрения квантового реактивного осциллятора и тогда не произошло. Годом позже Якимаха (1989) ^[3] рассмотрел пример последовательно-параллельного соединения квантовых 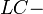$LC - \$ контуров (вернее их импедансов) при объяснении КЭХ (целочисленного и дробного). Но в этой работе не рассматривалась физическая сущность этих квантовых реактивных параметров а также не рассматривалось и квантовое уравнение Шредингера для реактивного осциллятора. Впервые одновременное рассмотрение всех квантовых реактивных параметров было осуществлено в работе Якимахи (1994) ^[4], при спектроскопических исследованиях МДП-транзисторов на низких частотах (звуковой диапазон). Плоские квантовые емкости и индуктивности здесь имели толщину равную Комптоновской длине волны электрона, а характеристическое сопротивление – волновому сопротивлению вакуума. Тремя годами позже Деворет (1997) ^[5] представил полную теорию квантового реактивного осциллятора (применительно к эффекту Джозефсона). Применение квантовых реактивных параметров в квантовом компьютинге освещено в работе Деворет (2004) ^[6].

Классический электромагнитный резонатор

В общем случае классический электромагнитный резонатор (КлЭР) являет собою полость в 3D-просторанстве. Поэтому КлЭР имеет бесконечное количество резонансных частот, обусловленных трехмерностью пространства. Например, прямоугольный КлЭР имеет следующие резонансные частоты:

$\omega_{mnp} = \frac{1}{\sqrt{\epsilon_0 \epsilon \mu_0 \mu}}\sqrt{(\frac{m\pi}{a})^2 + (\frac{n\pi}{b})^2 + (\frac{p\pi}{l}^2)}, \$

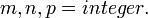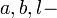где $m,n,p = integer. \$; $a, b, l - \$ соответственно ширина, толщина и длина, 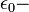$\epsilon_0- \$ диэлектрическая постоянная, 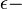$\epsilon- \$ относительная проницаемость, 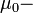$\mu_0 - \$ магнитная постоянная, 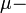$\mu - \$ относительная восприимчивость. В противоположность до классического LC контура, в КлЭР электрические и магнитные поля размещены в одном и том же объеме пространства. Эти осциллирующие электромагнитные поля в классическом случае формируют электромагнитные волны, которые могут быть излучены во внешний мир за пределы резонатора. Сегодня КлЭР широко используются в радиочастотном диапазоне волн (сантиметры и дециметры). Более того, КлЭР также используется в квантовой электронике, которая имеет дело с монохромными световыми волнами.

Квантовый подход

Квантовый LC контур

В классической физике мы имеем следующие соотношения соответствия между механическими и электродинамическими физическими параметрами:

магнитной индуктивностью и механической массой:

$L \leftrightarrow m \$;

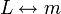электрической емкостью и обратной упругостью:

$C \leftrightarrow 1/k \$;

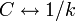электрическим зарядом и смещением координаты:

$q \leftrightarrow x \$.

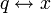Квантовый оператор импульса в зарядовом пространстве может быть представлен в следующем виде:

$\hat p_L = -i\hbar \frac{d}{dq}, \hat p_L^* = i\hbar \frac{d}{dq}, \$

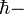где $\hbar- \$ приведенная постоянная Планка, 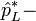$\hat p_L^*- \$ is the complex- комплексно сопряженный оператор импульса. Оператор Гамильтона в зарядовом пространстве может быть представлен как:

$\hat H_L = -\frac{\hbar^2}{2L}\frac{d^2}{dq^2} + \frac{L\omega_0^2}{2}\hat q^2, \$

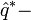где $\hat q^* - \$ комплексно сопряженный зарядовый оператор, и 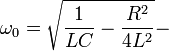$\omega_0 = \sqrt{\frac{1}{LC} - \frac{R^2}{4L^2}} - \$ резонансная частота. Рассмотрим случай без диссипации энергии (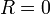$R = 0 \$). Единственное отличие между зарядовым пространством и традиционным 3D- координатным просторанством состоит в его одномерности (1D). Уравнение Шредингера для квантового LC контура может быть определено как:

$-\frac{\hbar^2}{2L}\frac{d^2 \Psi}{dq^2} + \frac{L\omega_0^2}{2}q^2\Psi = W\Psi. \$

Для решения этого уравнения необходимо ввести следующие безразмерные переменные:

$\xi = \sqrt{\frac{a}{b} = \frac{a}{b}} \$

$\lambda = \frac{2W}{\hbar\omega_0}, \$

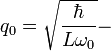где $q_0 = \sqrt{\frac{\hbar}{L\omega_0}}- \$ масштабный "заряд". Тогда уравнение Шредингера принимает форму дифференциального уравнения Чебышева-Эрмита:

$(\frac{d^2}{d\xi^2} + \lambda - \xi^2)\Psi = 0. \$

Собственные значения для оператора Гамильтона будут:

$W_n = \hbar \omega_0(n + 1/2), \$

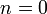где при $n = 0 \$ будем иметь нулевые осцилляции:

$W_0 = \hbar \omega_0/2. \$

В общем случае масштабный заряд может быть переписан в форме:

$q_0 = \sqrt{\frac{\hbar}{L\omega_0}} = \frac{q}{\sqrt{4\pi \alpha }}, \$

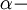где $\alpha - \$ постоянная тонкой структуры. Очевидно, что масштабный заряд отличается от "металлургического" заряда электрона. Более того, его квантизация будет иметь вид:

$q_{0n} = q_0\sqrt{2n +1}, n = 0,1,2,... \$.

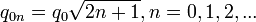Резонатор, как квантовый LC контур

Подход Лурия с использованием плотности энергетических состояний (ПЭС), дает следующее определение для квантовой емкости:

$C_{QR} = q_R^2\cdot D_{2D}\cdot S_R, \$

и квантовой индуктивности:

$L_{QR} = \phi_R^2\cdot D_{2D}\cdot S_R, \$

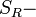где $S_R - \$ площадь поверхности резонатора, и 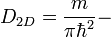$D_{2D} = \frac{m}{\pi \hbar^2} - \$ ПЭС в двухмерном пространстве (2D), 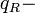$q_R - \$ электрический заряд (или поток), и 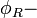$\phi_R - \$ магнитный заряд (или поток). Необходимо отметить, что эти потоки будут определены позже с помощью дополнительных условий.

Энергия накопленная на квантовой емкости:

$W_{CR} = \frac{q_R^2}{2D_{2D}S_R}. \$

Энергия накопленная на квантовой индуктивности:

$W_{LR} = \frac{\phi_R^2}{2D_{2D}S_R} = W_{CR}. \$

Угловая частота резонатора:

$\omega_{QR} = \frac{1}{\sqrt{L_{QR}C_{QR}}} = \frac{1}{q_R\phi_RD_{2D}S_R}. \$

Закон сохранения энергии:

$W_{QR} = \hbar \omega_R = \frac{1}{q_R\phi_RD_{2D}S_R} = W_{CR} = W_{LR}. \$

Это уравнение может быть переписано как:

$q_R\phi_R = \hbar, \$

с которого видно, что эти „заряды” есть в действительности „потоки поля”, а не „металлургические заряды”.

Характеристический импеданс резонатора:

$\rho_{QR} = \sqrt{\frac{L_{QR}}{C_{QR}}} = \frac{\phi_R}{q_R} = \begin{cases} 2\frac{\phi_0}{e}=2R_H, & \mbox{for QHE } \\ 2\alpha \frac{\phi_0}{e}=2\alpha R_H, & \mbox{for other } \end{cases} \$

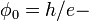где $\phi_0 = h/e - \$ квант магнитного потока.

Из приведенных выше уравнений мы можем найти следующие значения электрического и магнитного потоков поля:

$q_R = \begin{cases} q_{R1} = \frac{e}{\sqrt{2\pi}}, & \mbox{for QHE } \\ q_{R2} = \frac{e}{\sqrt{2\pi \alpha}}, & \mbox{for other } \end{cases} \$

$\phi_R = \begin{cases} \phi_{R1} = \frac{\phi_0}{\sqrt{\frac{2}{\pi}}}, & \mbox{for QHE } \\ \phi_{R2} = \frac{\phi_0}{\sqrt{\frac{2\alpha}{\pi}}}, & \mbox{for other } \end{cases} \$

Необходимо еще раз напомнить, что эти величины не являются „металлургическими зарядами”, но максимальными амплитудными значениями потоков поля, которые поддерживают энергетический баланс между энергией осцилляций резонатора и полной энергией на емкости и индуктивности:

$\hbar \omega_{QR} = W_{QL}(t) + W_{QC}(t). \$

Поскольку осцилляции на емкости смещены по фазе (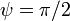$\psi = \pi /2 \$) по отношению к осцилляциям на индуктивности, поэтому мы будем иметь:

$W_{QL} = \begin{cases} 0, & \mbox{at }t=0; \psi=0\mbox{ and} t=\frac{T_{QR}}{2};\psi=\pi \\ W_{QL}, & \mbox{at }t=\frac{T_{QR}}{4};\psi=\frac{\pi}{4} \mbox{ and}t=\frac{3T_{QR}}{4};\psi=\frac{3\pi}{4} \end{cases} \$

$W_{QC} = \begin{cases} W_{QC}, & \mbox{at }t=0; \psi=0\mbox{ and} t=\frac{T_{QR}}{2};\psi=\pi \\ 0, & \mbox{at }t=\frac{T_{QR}}{4};\psi=\frac{\pi}{4} \mbox{ and}t=\frac{3T_{QR}}{4};\psi=\frac{3\pi}{4} \end{cases} \$

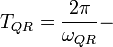где $T_{QR} = \frac{2\pi}{\omega_{QR}}- \$ период осцилляций.

См. также

• Резонатор
• Квантовый зарядовый осциллятор
• Квантовая емкость
• Квантовая индуктивность (графен)

Ссылки

1. ↑ Louisell W. H. (1973). “Quantum Statistical Properties of Radiation”. Wiley, New York.
2. ↑ Serge Luryi (1988). "Quantum capacitance device". Appl.Phys.Lett. 52(6). Pdf
3. ↑ Yakymakha O.L.(1989). High Temperature Quantum Galvanomagnetic Effects in the Two- Dimensional Inversion Layers of MOSFET's (In Russian). Kyiv: Vyscha Shkola. p.91. ISBN 5-11-002309-3. djvu</
4. ↑ Yakymakha O.L., Kalnibolotskij Y.M. (1994). "Very-low-frequency resonance of MOSFET amplifier parameters". Solid- State Electronics 37(10),1739-1751 Pdf
5. ↑ Deboret M.H. (1997). "Quantum Fluctuations". Amsterdam, Netherlands: Elsevier. pp.351-386. Pdf
6. ↑ Devoret M.H., Martinis J.M. (2004). "Implementing Qubits with Superconducting Integrated Circuits". Quantum Information Processing, v.3, N1. Pdf

Литература

• Stratton J.A.(1941). Electromagnetic Theory. New York, London: McGraw-Hill.p.615. djvu
• Детлаф А.А., Яворский Б.М., Милковская Л.Б.(1977). Курс физики. Том 2. Электричество и магнетизм (4-е издание). М.: Высшая школа, "Reference Book on Electricity" djvu
• Гольдштейн Л.Д., Зернов Н.В. (1971). Электромагнитные поля. 2- издание. Москва: Советское Радио. 664с. "Electromagnetic Fields" djvu