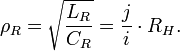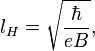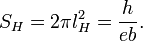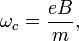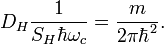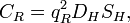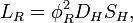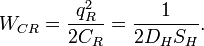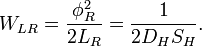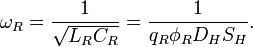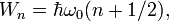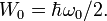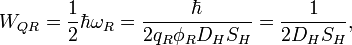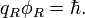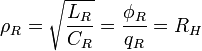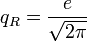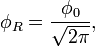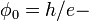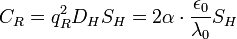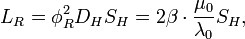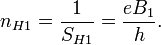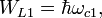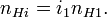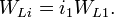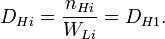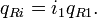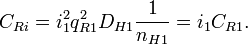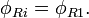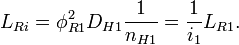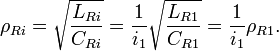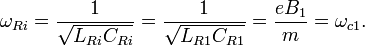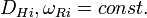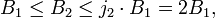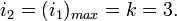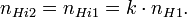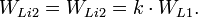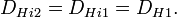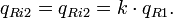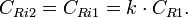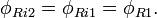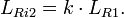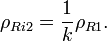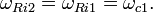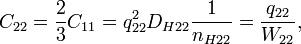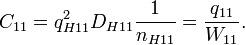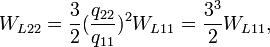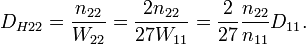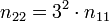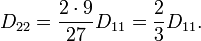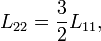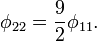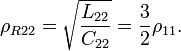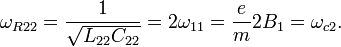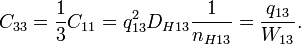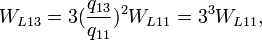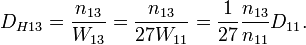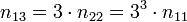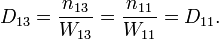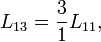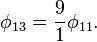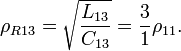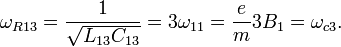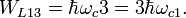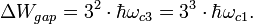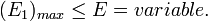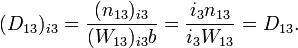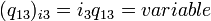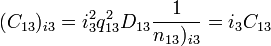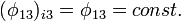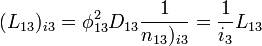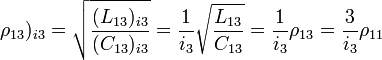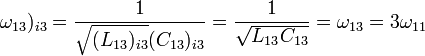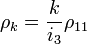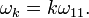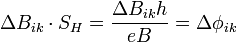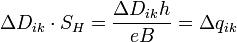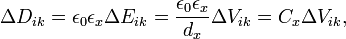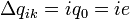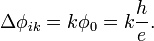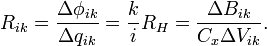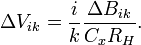- Квантовый композитный резонатор Холла
-
Квантовый композитный резонатор Холла
Квантовый композитный резонатор Холла (ККРХ) — топологический объект с квантовыми реактивными параметрами (
 и
и  ), которые имеют фиксированную резонансную частоту (
), которые имеют фиксированную резонансную частоту ( ), обусловленную нечетным числом электронов которые двигаются в однородном магнитном поле (
), обусловленную нечетным числом электронов которые двигаются в однородном магнитном поле (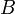 ). ККРХ имеет характеристический импеданс пропорциональный постоянной Клитцинга (
). ККРХ имеет характеристический импеданс пропорциональный постоянной Клитцинга (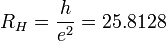 кОм), нечетному числу электронов (
кОм), нечетному числу электронов (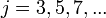 ), и обратно пропорционально числу уровней (
), и обратно пропорционально числу уровней (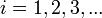 ):
):Содержание
История
Открытие квантового эффекта Холла Клитцингом (1980) [1] было абсолютно неожиданным для физического сообщества, поскольку никто не предполагал, что такая макроскопическая величина, как сопротивление (проводимость) может квантоваться.
Простая квантовая теория, предложенная Лафлином [2] свела квантизацию сопротивления к одноэлектронному заполнению уровней Ландау в сильном магнитном поле, что вынуждает электроны двигаться по замкнутой круговой траектории в 2М-плоскости. Более того, т. н. холловский ток в этом подходе определяется через адиабатическую производную от полной энергии системы по магнитному потоку, протекающему через замкнутую петлю. Необходимо отметить, что этот подход не учитывает electric field коллинеарное магнитному полю, которое может быть достаточно сильным (особенно в МДН-транзисторах), а также не учитывает реактивные параметры формируемой по умолчанию Quantum LC Circuit.
Ситуация в значительной мере усложнилась с открытием Стормером, Цуи и Госсардом [3] дробного КЭХ. Сравнительно простая теоретическая модель, предложенная Лафлином в этом случае по умолчанию рассматривает дробное значение электрического заряда [4], которое в дальнейшем было названо Джайном (1989) [5]. композитными фермионами. Дальнейшее развитие этого подхода было сделано Симоном (1998) [6]. Следует отметить, что в рамках этого пордхода уровни Ландау заполняются composite fermions, которые имеют дробные заряды, и другие недостатки, присущие для подхода Лафлина для КЭХ.
Подход Лафлина-Джайна-Симона сегодня доминирует при рассмотрении гальваномагнитных явлений, но некоторые физики достаточно критически к ней относятся. Например, Шривастава [7] считает, что концепция композитных фермионов по умолчанию принимает существование квантовых магнитных потоков φ0 = h / e как независимых частиц, которые могут быть связаны с электроном, формируя композитное сосояние с некоторыми квантами электрического и магнитного потока. Теория таких композитных фермионов не может быть успешно сформулируема исходя из первичных принципов.
Более того, M.I. Dyakonov (2002) [8] писал, что сегодня физики находятся в неудобном положении: с одной стороны существует многочисленное количество экспериментальных фактов, что подтверждают «идею» композитных фермионов, которые принимают участие в этом «единственном» подходе к существующему явлению. Также очевидно, что эта идея отражает некоторую реальность., но с другой стороны, никто не доказал теоретически существование композитных фермионов, как свободных квази-частиц.В действительности существует другой подход (хотя и менее популярный) к проблеме дробного КЭХ. Вначале 21-го века появилась новая концепция квантовой механики, предложенная Тсу [9], [10] в котором характеристический импеданс играет доминантную роль. Важность учета характеристического импеданса в квантовом осцилляторе показана Зельдовичем (2008) [11]. Но Тсу и Зельдович не были первыми в этом вопросе. Поэтому имеет смысл остановиться на истории квантовых реактивных параметров подробнее.
Так сложилось исторически, что физические реактивные величины такие, как емкость и индуктивность практически не рассматривались не только в квантовой, но даже и в классической теоретической электродинамике. Дело в том, что последние не входят в явном виде в систему уравнений Максвелла, в результате решения которой всегда получались электромагнитные поля, и если иногда в получаемых решениях и возникали размерные коэффициенты, которые можно было связать с емкостью или индуктивностью, то и отношение к ним было соответствующее. Не менее известно также, что «полевой подход» приводит к появлению «дурных бесконечностей», обусловленных рассмотрением движения «математической точки» (с электрическим зарядом) под воздействием силовых полей. Не избежала «дурных бесконечностей» и общепризнанная квантовая электродинамика, в рамках которой были также разработаны мощные методы «компенсации дурных бесконечностей».
Напротив, в прикладной физике понятие емкости и индуктивности нашло широкое применение, сначала в электротехнике, а потом в радиоэлектронике. Основным результатом применения реактивных параметров в прикладной физике является сегодня широкое распространение информационных технологий, которые базируются на генерации, приеме и передаче электромагнитных волн на различной частоте. В тоже время неразработанность на теоретическом уровне физических понятий для емкости и индуктивности сегодня уже становится в определенной мере сдерживающим фактором в развитии информационных технологий вообще и квантового компьютинга в частности. Достаточно вспомнить, что квантовое рассмотрение классического механического осциллятора было реализовано в эпоху создания квантовой механики (как одна из иллюстраций ее практического применения), тогда как квантовое рассмотрение
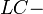 контура было теоретически поставлено только в начале 70-х годов 20-го века а детальное рассмотрение началось только в средине 90-х годов.
контура было теоретически поставлено только в начале 70-х годов 20-го века а детальное рассмотрение началось только в средине 90-х годов.Впервые необходимость решения уравнения Шредингера для квантового
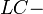 контура была поставлена в монографии Луизелла (1973) [12]. Поскольку тогда еще не было понимания, что собой представляют квантовые реактивные параметры (да и практических примеров тогда не было), то поэтому широкого распространения данный подход не получил. Теоретически корректное введение квантовой емкости, которое базировалось на плотности состояний впервые введено Лурием (1988) [13] при рассмотрении квантового эффекта Холла (КЭХ). К сожалению тогда не были введены квантовые индуктивности, которые также вытекали из плотности состояний, и поэтому полноценного рассмотрения квантового реактивного осциллятора и тогда не произошло. Годом позже Якимаха (1989) [14] рассмотрел пример последовательно-параллельного соединения квантовых
контура была поставлена в монографии Луизелла (1973) [12]. Поскольку тогда еще не было понимания, что собой представляют квантовые реактивные параметры (да и практических примеров тогда не было), то поэтому широкого распространения данный подход не получил. Теоретически корректное введение квантовой емкости, которое базировалось на плотности состояний впервые введено Лурием (1988) [13] при рассмотрении квантового эффекта Холла (КЭХ). К сожалению тогда не были введены квантовые индуктивности, которые также вытекали из плотности состояний, и поэтому полноценного рассмотрения квантового реактивного осциллятора и тогда не произошло. Годом позже Якимаха (1989) [14] рассмотрел пример последовательно-параллельного соединения квантовых 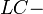 контуров (вернее их импедансов) при объяснении КЭХ (целочисленного и дробного). Но в этой работе не рассматривалась физическая сущность этих квантовых реактивных параметров а также не рассматривалось и квантовое уравнение Шредингера для реактивного осциллятора. Впервые одновременное рассмотрение всех квантовых реактивных параметров было осуществлено в работе Якимахи (1994) [15], при спектроскопических исследованиях МДП-транзисторов на низких частотах (звуковой диапазон). Плоские квантовые емкости и индуктивности здесь имели толщину равную Комптоновской длине волны электрона, а характеристическое сопротивление — волновому сопротивлению вакуума. Тремя годами позже Деворет (1997) [16] представил полную теорию квантового реактивного осциллятора (применительно к эффекту Джозефсона). Применение квантовых реактивных параметров в квантовом компьютинге освещено в работе Деворет (2004) [17].
контуров (вернее их импедансов) при объяснении КЭХ (целочисленного и дробного). Но в этой работе не рассматривалась физическая сущность этих квантовых реактивных параметров а также не рассматривалось и квантовое уравнение Шредингера для реактивного осциллятора. Впервые одновременное рассмотрение всех квантовых реактивных параметров было осуществлено в работе Якимахи (1994) [15], при спектроскопических исследованиях МДП-транзисторов на низких частотах (звуковой диапазон). Плоские квантовые емкости и индуктивности здесь имели толщину равную Комптоновской длине волны электрона, а характеристическое сопротивление — волновому сопротивлению вакуума. Тремя годами позже Деворет (1997) [16] представил полную теорию квантового реактивного осциллятора (применительно к эффекту Джозефсона). Применение квантовых реактивных параметров в квантовом компьютинге освещено в работе Деворет (2004) [17].Общий подход к проблеме квантового резонатора
Квантвый резонатор Холла (КРХ)
Магнитная длина:
где
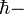 приведенная постоянная Планка,
приведенная постоянная Планка, 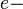 заряд электрона, и
заряд электрона, и 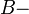 внешнее однородное магнитное поле.
внешнее однородное магнитное поле.Масштабный параметр поверхности:
Циклотронная частота:
где
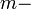 эффективная масса электрона в твердом теле.
эффективная масса электрона в твердом теле.КРХ плотность энергетических состояний (ПЭС):
где qR − электрический поток через поверхность
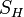 . ПЭС квантовая индуктивность:
. ПЭС квантовая индуктивность:где φR − магнитный поток через поверхность
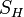 . Учитывая квантовые осцилляции в резонаторе, эти потоки являются только «амплитудными значениями», и они не квантуются подобно «металлургическим зарядам». Максимальное значение энергии на емкости:
. Учитывая квантовые осцилляции в резонаторе, эти потоки являются только «амплитудными значениями», и они не квантуются подобно «металлургическим зарядам». Максимальное значение энергии на емкости:Максимальное значение энергии на индуктивности:
КХР резонансная частота:
Стандартный квантовый осциллятор имеет следующие собственные значения для оператора Гамильтона:
где при
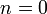 будем иметь нулевые колебания:
будем иметь нулевые колебания:Закон сохранения энергии при (n = 0):
который приводит к следующему взаимосоотношению между потоками (некоторый аналог соотношения неопределенностей Гейзенберга для потоков).
КХР характеристический импеданс:
Решение этих двух уравнений дает следующие значения для электрического и магнитного потоков:
где
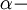 электрическая постоянная тонкой структуры,
электрическая постоянная тонкой структуры, 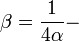 магнитная постоянная тонкой структуры,
магнитная постоянная тонкой структуры, 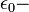 диэлектрическая постоянная,
диэлектрическая постоянная, 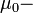 магнитная постоянная, и
магнитная постоянная, и 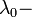 Комптоновская длина волны электрона. Необходимо отметить, что резонансная частота КРХ принимает значение циклотронной частоты здесь:
Комптоновская длина волны электрона. Необходимо отметить, что резонансная частота КРХ принимает значение циклотронной частоты здесь:Формирование квантового композитного резонатора
Прямой ход
Рассмотрим стандартный КЭХ с одноэлектронным заполнением уровней Ландау шаг за шагом в постоянном однородном магнитном поле
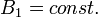 и медленно увеличивающемся электрическом поле
и медленно увеличивающемся электрическом поле 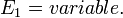 Поверхностная концентрация электронов на первом уровне Ландау будет:
Поверхностная концентрация электронов на первом уровне Ландау будет:Энергия первого уровня Ландау:
где
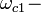 циклотронная частота, обусловленная магнитным полем
циклотронная частота, обусловленная магнитным полем  .
.С увеличением чисел заполнения
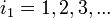 мы будем иметь следующие значения параметров КХР: Поверхностная концентрация электронов:
мы будем иметь следующие значения параметров КХР: Поверхностная концентрация электронов:Энергия уровней Ландау:
Плотность энергетических состояний (ПЭС):
Индуцированный электрический поток:
ПЭС квантовая емкость:
Таким образом, мы имеем параллельное соединение квантовых емкостей «элементарных резонаторов» в этом случае.
Индуцированный магнитный поток:
ПЭС квантовая индуктивность:
Таким образом, мы здесь имеем последовательное соединение квантовых индуктивностей «элементарных резонаторов» в этом случае.
Характеристический импеданс:
Резонансная частота:
Таким образом, в постоянном однородном магнитном поле с одноэлектронным заполнением уровней Ландау мы будем иметь следующие значения параметров:
Обратный ход
Рассмотрим обратный ход, когда электрическое поле постоянно (
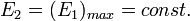 ), а магнитное поле медленно растет:
), а магнитное поле медленно растет:где
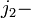 максимальное значение числа электронов на уровне Ландау (или целое число, которое учитывает уменьшение масштабного поверхностного параметра).
максимальное значение числа электронов на уровне Ландау (или целое число, которое учитывает уменьшение масштабного поверхностного параметра).Максимальное значение числа заполненных уровней Ландау для прямого хода (или число электронов участвующих в КЭХ):
С целью унификации рассмотрения необходимо переобозначить параметры прямого хода для будущего композитного резонатора. Поверхносная концентрация электронов:
Энергия уровня Ландау:
Плотность энергетических состояний:
Индуцированный электрический поток:
Квантовая емкость:
Индуцированный магнитный поток:
Квантовая индуктивность:
Характеристический импеданс:
Резонансная частота:
Таким образом, мы готовы к рассмотрению второго шага рассмотрения при
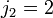 ,
, 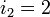 и
и 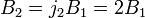 . Следует отметить, что с увеличением магнитного поля до значения
. Следует отметить, что с увеличением магнитного поля до значения 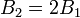 второй электрон со второго уровня Ландау перемещается на первый уровень, заполненный первым электроном, а третий электрон переходит на второй уровень Ландау. Таким образом, мы здесь имеем композитный резонатор с двумя заполненными уровнями Ландау.
второй электрон со второго уровня Ландау перемещается на первый уровень, заполненный первым электроном, а третий электрон переходит на второй уровень Ландау. Таким образом, мы здесь имеем композитный резонатор с двумя заполненными уровнями Ландау.Квантовая ПЭХ емкость в этом случае принимает вид:
где
Полная энергия этого композитного резонатора будет:
при
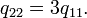
Плотность энергетических состояний:
Естесственное предположение для поверхностной плотности электронов
дает следующее значение для ПЭС:
Квантовая ПЭС индуктивность:
где учтен индуцированный магнитный поток:
Характеристический импеданс в этом случае будет:
Резонансная частота:
Теперь мы готовы к рассмотрению завершального третьего случая при
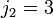 ,
, 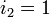 и
и 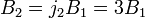 . Следует помнить, что с увеличением магнитного поля до
. Следует помнить, что с увеличением магнитного поля до 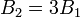 третий электрон со второго уровня Ландау переходит на первый уровень, заполненный первым и вторым электронами. Таким образом, мы получили искомый композитный резонатор с одним уровнем Ландау, заполненным тремя электронами. Квантовая емкость композитного резонатора здесь будет:
третий электрон со второго уровня Ландау переходит на первый уровень, заполненный первым и вторым электронами. Таким образом, мы получили искомый композитный резонатор с одним уровнем Ландау, заполненным тремя электронами. Квантовая емкость композитного резонатора здесь будет:Полная энергия этого композитного резонатора:
при
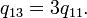 Плотность энергетических состояний:
Плотность энергетических состояний:Естесственное предположение для поверхностной плотности электронов
приводит к следующему значению для ПЭС в этом случае:
Таким образом, новая композитная система возвращается в исходное двумерное состояние (или система ККР возвращается в «начало»).
Квантовая индуктивность композитного резонатора::
где учтен индуцированный магнитный поток:
Характеристический импеданс здесь будет:
Резонансная частота:
Итак, квантовый композитный резонатор Холла сформирован. Энергия на один уровень Ландау:
Энергетическая щель для ККРХ:
Теперь ККРХ может рассматриваться как целостный элементарный объект по отношению к внешнему магнитному и электрическому полю, независимо от его внутренней структуры. Следует напомнить, что этот элементарный объект связан с тремя металлургическими электронами которые изменяют свое состояние одновременно.
ККРХ и дробный КЭХ
Теперь мы можем рассмотреть т. н. дробный КЭХ с помощью модели композитного резонатора, сформированного тремя электронами. Также как и одноэлектронном резонаторе мы должны зафиксировать магнитное поле:
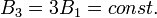 ,
,
и постепенно увеличивать электрическое поле:
Таким образом, число заполнения уровней Ландау здесь будет
связано с тремя электронами для каждого уровня Ландау. Поверхностная плотность электронов здесь будет:
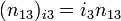 ,
,
а плотность состояний:
Индуцированный электрический поток:
ПЭС квантовая емкость:
Индуцированный магнитный поток:
ПЭС квантовая индуктивность:
Характеристический импеданс здесь будет:
где
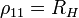 ККРХ резонансная частота:
ККРХ резонансная частота:Необходимо отметить, что в общем случае число заполнения :
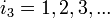 может быть связано с любым нечетным числом заполнения электронов на уровень Ландау (
может быть связано с любым нечетным числом заполнения электронов на уровень Ландау (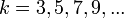 ). Но, в этом случае мы будем иметь другие величины для характеристического импеданса и резонансной частоты:
). Но, в этом случае мы будем иметь другие величины для характеристического импеданса и резонансной частоты:Квантовая антиточка
Резонансное туннелирование электронов [18] в квантовой антиточке Голдмана [19] может быть исследовано экспериментально путем измерения периодического квантования (осцилляций) магнитного или электрического полей:
где
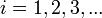 — число уровней Ландау, и
— число уровней Ландау, и 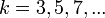 — число электронов в композитном резонаторе.
— число электронов в композитном резонаторе.Электрическое поле в квантовой антиточке может быть представлено через приложенное напряжение:
где
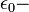 диэлектрическая константа,
диэлектрическая константа, 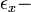 относительная проницаемость гетероперехода,
относительная проницаемость гетероперехода, 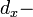 толщина гетероперехода, и
толщина гетероперехода, и 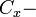 мезоскопическая емкость гетероперехода на единицу площади.
мезоскопическая емкость гетероперехода на единицу площади.Квантизация электрических и магнитных потоков обусловлена свойствами композитного резонатора, сформированного в в квантовой антиточке:
Характеристический импеданс quantum antidot Characteristic impedance of композитного резонатора:
Теперь можно найти взаимосвязь между кванизацией электрического напряжения и магнитного поля:
Таким образом, нету никаких дробных электрических зарядов в квантовой антиточке. Количество туннелировавших электронов обусловлено числом уровней Ландау (
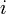 ). НО количество квантов магнитного потока обусловлено числом электронов в композитном резонаторе (
). НО количество квантов магнитного потока обусловлено числом электронов в композитном резонаторе (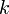 ).
).Смотри также
- Квантовый электромагнитный резонатор
- Квантовый LC контур
- Квантовая емкость
- Квантовая индуктивность (графен)
- Квантовый эффект Холла
- Дробный квантовый эффект Холла
Ссылки
- ↑ Klitzing, K. von; Dorda, G.; Pepper, M. (1980). "New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance". Phys. Rev. Lett. 45 (6): 494–497. DOI:10.1103/PhysRevLett.45.494.
- ↑ Laughlin, R. B. (1981). "Quantized Hall conductivity in two dimensions". Phys. Rev. B. 23 (10): 5632–5633. DOI:10.1103/PhysRevB.23.5632.
- ↑ D.C. Tsui, H.L. Stormer, and A.C. Gossard, Phys. Rev. Lett. 48, 1559 (1982) DOI:10.1103/PhysRevLett.48.1559
- ↑ R.B. Laughlin, Phys. Rev. Lett. 50, 1395 (1983) DOI:10.1103/PhysRevLett.50.1395
- ↑ J.K. Jain, Phys. Rev. Lett. 63, 199 (1989); Phys. Rev. B 40, 8079 (1989); Phys. Rev. B 41, 7653 (1990)
- ↑ S.H. Simon, The Chern-Simons Fermi Liquid Description of Fractional Quantum Hall states, ibid; LANL e-print cond-mat/9812186, (1998)
- ↑ Keshav N. Shrivastava. Comments on "Composite Fermions (CF) model of quantum Hall effect — Two-dimensional electron system in high magnetic fields, S. S. Mandal, M. R. Peterson and J. K. Jain, Phys. Rev. Lett. 90, 106403 (2003) PDF
- ↑ M.I. Dyakonov, Twenty years since the discovery of the Fractional Quantum Hall Effect: Current state of the theory. Condensed Matter, 9 Sep 2002 PDF
- ↑ Timir Datta, Raphael Tsu (2003). Quantum Wave Resistance of Schrodinger functions. PDF
- ↑
- ↑ Boris Ya. Zel’dovich. Impedance and parametric excitation of oscillators. UFN, 2008, v. 178, No 5 PDF
- ↑ Louisell W. H. (1973). «Quantum Statistical Properties of Radiation». Wiley, New York.
- ↑ Serge Luryi (1988). «Quantum capacitance device». Appl.Phys.Lett. 52(6). Pdf
- ↑ Yakymakha O.L.(1989). High Temperature Quantum Galvanomagnetic Effects in the Two- Dimensional Inversion Layers of MOSFET’s (In Russian). Kyiv: Vyscha Shkola. p.91. ISBN 5-11-002309-3. djvu</
- ↑ Yakymakha O.L., Kalnibolotskij Y.M. (1994). «Very-low-frequency resonance of MOSFET amplifier parameters». Solid- State Electronics 37(10),1739-1751 Pdf
- ↑ Deboret M.H. (1997). «Quantum Fluctuations». Amsterdam, Netherlands: Elsevier. pp.351-386. Pdf
- ↑ Devoret M.H., Martinis J.M. (2004). «Implementing Qubits with Superconducting Integrated Circuits». Quantum Information Processing, v.3, N1. Pdf
- ↑ S. Luryi, A. Zaslavsky. CHAPTER 5. QUANTUM-EFFECT AND HOT-ELECTRON DEVICES
- ↑ V.J.Goldman and B.Su «Resonant Tunneling in Quantum Hall Effect: Measurement of Fractional Charge». Science 267, 1010—1012 (1995)
Литература
- Stratton J.A.(1941). Electromagnetic Theory. New York, London: McGraw-Hill.p.615. djvu
- Детлаф А. А., Яворский Б. М., Милковская Л. Б.(1977). Курс физики. Том 2. Электричество и магнетизм (4-е издание). М.: Высшая школа, «Reference Book on Electricity» djvu
- Гольдштейн Л. Д., Зернов Н. В. (1971). Электромагнитные поля. 2- издание. Москва: Советское Радио. 664с. «Electromagnetic Fields» djvu
- Zyun F. Ezawa: Quantum Hall Effects — Field Theoretical Approach and Related Topics. World Scientific, Singapore 2008, ISBN 978-981-270-032-2
- Sankar D. Sarma, Aron Pinczuk: Perspectives in Quantum Hall Effects. Wiley-VCH, Weinheim 2004, ISBN 978-0-471-11216-7
- Composite Fermions, Edited by O. Heinonen, World Scientific, Singapore (1998).
Wikimedia Foundation. 2010.
Квантовый эффект Холла — Квантовый эффект Холла эффект квантования холловского сопротивления или проводимости двумерного электронного газа в сильных магнитных полях и при низких температурах. Квантовый эффект Холла (КЭХ) был открыт Клаусом фон Клитцингом (совместно … Википедия
Квантовый эффект холла — эффект квантования холловского сопротивления или проводимости двумерного электронного газа в сильных магнитных полях и при низких температурах. Квантовый эффект Холла (КЭХ) был открыт Клаусом фон Клитцингом (совместно с Г. Дордой и М. Пеппером) в … Википедия
Дробный квантовый эффект Холла — Дробный квантовый эффект Холла одно из проявлений квантового эффекта Холла, когда при дробных числах заполнения уровней Ландау в двумерном электронном газе на графической зависимости холловского сопротивления от величины магнитной индукции… … Википедия
КЭХ — Квантовый эффект Холла эффект квантования холловского сопротивления или проводимости двумерного электронного газа в сильных магнитных полях и при низких температурах. Квантовый эффект Холла (КЭХ) был открыт Клаусом фон Клитцингом (совместно с Г.… … Википедия