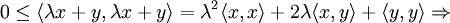КБШ

Неравенство Коши́ — Буняко́вского связывает норму и скалярное произведение векторов в линейном пространстве. Это неравенство эквивалентно неравенству треугольника для нормы в пространстве со скалярным произведением.

Неравенство Коши — Буняковского иногда, особенно в иностранной литературе, называют неравенством Шварца, хотя работы Шварца (нем.) на эту тему появились только спустя 25 лет после работ Буняковского^[1]. Конечномерный случай этого неравенства называется неравенством Коши и был доказан Коши в 1821 году.

Формулировка

Пусть дано линейное пространство L со скалярным произведением 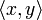$\langle x, y \rangle$. Пусть 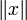$\|x\|$ — норма, порождённая скалярным произведением, то есть 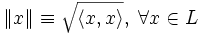$\|x\| \equiv \sqrt{\langle x, x \rangle},\; \forall x \in L$. Тогда для любых 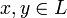$x,y\in L$ имеем

$|\langle x, y\rangle| \le \|x\| \cdot \|y\|$,

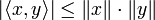причём равенство достигается тогда и только тогда, когда векторы x и y пропорциональны (коллинеарны).

Комментарии

В конечномерном случае можно заметить, что 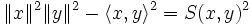$\|x\|^2\|y\|^2 - \langle x, y\rangle^2 = S(x,y)^2$, где S(x,y) — площадь параллелограмма, натянутого на векторы x и y.

В общем случае $\|x\|^2- {\langle x, y\rangle^2\over \|y\|^2} = \|x - {\langle x,y\rangle \over\|y\|^2}y\|^2$

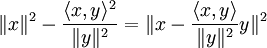
Примеры

• В пространстве комплекснозначных квадратично суммируемых последовательностей l² неравенство Коши — Буняковского имеет вид:

$\left| \sum\limits_{k=1}^{\infty} x_k \bar{y}_k \right| ^2 \le \left( \sum_{k=1}^{\infty} |x_k|^2 \right) \cdot \left( \sum_{k=1}^{\infty} |y_k|^2 \right)$,

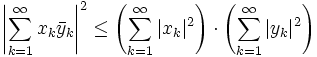где 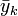$\bar{y}_k$ обозначает комплексное сопряжение y_k.

• В пространстве комплексных квадратично интегрируемых функций 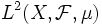$L^2(X,\mathcal{F},\mu)$ неравенство Коши — Буняковского имеет вид:

$\left|\int\limits_X f(x)\overline{g(x)}\,\mu(dx)\right|^2\leq \left(\int\limits_X \left|f(x)\right|^2\,\mu(dx)\right) \cdot \left(\int\limits_X\left|g(x)\right|^2\,\mu(dx)\right)$.

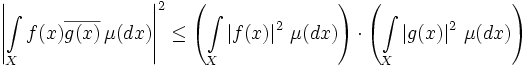• В пространстве случайных величин с конечным вторым моментом 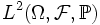$L^2(\Omega,\mathcal{F},\mathbb{P})$ неравенство Коши — Буняковского имеет вид:

$\mathrm{cov}^2(X,Y) \le \mathrm{D}[X] \cdot \mathrm{D}[Y]$,

где cov обозначает ковариацию, а D дисперсию.

Доказательство

$0\le\langle\lambda x+y,\lambda x+y\rangle=\lambda^2\langle x,x\rangle+2\lambda\langle x,y\rangle+\langle y,y\rangle \Rightarrow$

Значит дискриминант многочлена 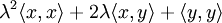$\lambda^2\langle x,x\rangle+2\lambda\langle x,y\rangle+\langle y,y\rangle$ неположительный, то есть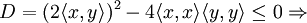

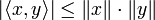$D=(2\langle x,y\rangle)^2-4\langle x,x\rangle\langle y,y\rangle\le 0\Rightarrow$

$|\langle x,y\rangle|\le \|x\|\cdot\|y\|$.

Литература

1. ↑ Bounjakowsky W., «Mémoires de l’Académie des sciences de St-Pétersbourg. 7 série», 1859, t. 1, № 9.