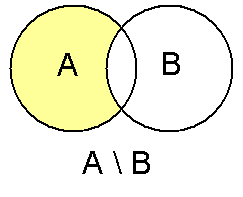
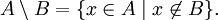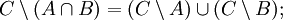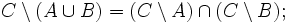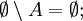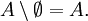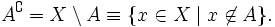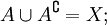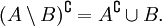Дополнение (теория множеств) — Дополнение в теории множеств это семейство элементов, не принадлежащих данному множеству. Содержание 1 Разность множеств 1.1 Определение 1.2 Примеры 1.3 Свойства … Википедия
Дополнение (математика) — Дополнение в теории множеств это семейство элементов, не принадлежащих данному множеству. Содержание 1 Разность множеств 1.1 Определение 1.2 Примеры 1.3 Свойства … Википедия
ДОПОЛНЕНИЕ — операция, к рая ставит в соответствие подмножеству Мданного множества Xдругое подмножество так, что если известны Ми N, то тем или иным способом может быть восстановлено множество X. В зависимости от того, какой структурой наделено множество X,… … Математическая энциклопедия
Дополнение графа — Граф Петерсена (слева) и его дополнение (справа). В теории графов дополнением или обратным к графу G называется такой граф H, имеющий то же множество вершин, что и G, но в котором две несовпадающие вершины смежны тогда и только тогда, когда они… … Википедия
дополнение к множеству — такое множество не А, когда A + не А = 1, где 1 обозначает некоторую предметную область (универсальный класс). Пусть A будет множеством млекопитающих, а областью нашего рассуждения будет множество позвоночных животных. Тогда дополнением к нему… … Словарь терминов логики
ДИЗЪЮНКТНОЕ ДОПОЛНЕНИЕ — множества А множество всех элементов х векторной решетки (векторной структуры) X, дизъюнктных множеству (см. Дизъюнктные элементы). кроме того, если X векторная условно полная решетка, то Add является наименьшей компонентой пространства X,… … Математическая энциклопедия
Плотные и неплотные множества — понятия множеств теории (См. Множеств теория). Множество Е называется плотным на М, если каждая точка множества М является предельной точкой (См. Предельная точка) Е, т. е. в любой окрестности имеются точки, принадлежащие Е. Плотные… … Большая советская энциклопедия
Мера множества — У этого термина существуют и другие значения, см. Мера. Мера множества неотрицательная величина, интуитивно интерпретируемая как размер (объем) множества. Собственно, мера это некоторая числовая функция, ставящая в соответствие каждому… … Википедия
КАТЕГОРИЯ МНОЖЕСТВА — топологическая характеристика массивности множества. Множество Етопологич. пространства Xназ. множеством первой категории на X, если оно представимо в виде конечной или счетной суммы множеств, нигде не плотных на X. В противном случае Еназ.… … Математическая энциклопедия
Существование перечислимого неразрешимого множества — В данной статье будет доказан теорема о существовании перечислимого, но неразрешимого множества. Напомню, что по теореме Поста перечислимое множества разрешимо тогда и только тогда, когда его дополнение перечислимо.Основные определения, такие как … Википедия
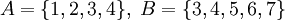 . Тогда
. Тогда 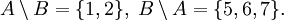
 — множество всех вещественных чисел,
— множество всех вещественных чисел, 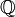 — множество рациональных чисел, а
— множество рациональных чисел, а  — множество целых чисел. Тогда
— множество целых чисел. Тогда 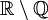 — множество всех иррациональных чисел, а
— множество всех иррациональных чисел, а 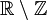 — дробных.
— дробных.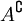 непусты, то
непусты, то 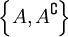 является разбиением X.
является разбиением X.