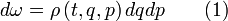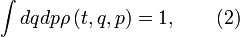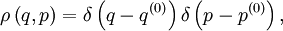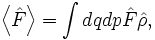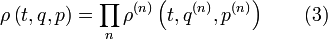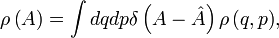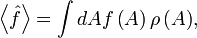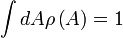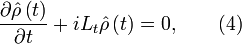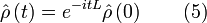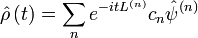- Функция распределения (статистическая механика)
-
Статистическая физика 
Термодинамика
Молекулярно-кинетическая теорияСтатистики Максвелла-Больцмана
Бозе-Эйнштейна · Ферми-Дирака
Parastatistics · Anyonic statistics
Braid statisticsАнсамбли Микроканонический ·Канонический
Большой канонический
Изотермо-изобарический
Изоэнатльпи-изобарическийТермодинамика Уравнение состояния · Цикл Карно ·Закон Дюлонга — Пти Модели Модель Дебая ·Эйнштейна ·Модель Изинга Потенциалы внутренняя энергия ·Энтальпия
Свободная энергия Гельмгольца
потенциал Гиббса · Большой термодинамический потенциалИзвестные учёные Максвелл ·Гиббс ·Больцман Функция статистического распределения (функция распределения в статистической физике) — одно из основополагающих понятий статистической физики. Знание функции распределения полностью определяет вероятностные свойства рассматриваемой системы.
Механическое состояние любой системы однозначно определяется координатами qi и импульсами pi ее частиц (i=1,2,…, d; d — число степеней свободы системы). Набор величин
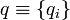 и
и 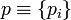 образуют фазовое пространство. Вероятность нахождения системы в элементе фазового пространства
образуют фазовое пространство. Вероятность нахождения системы в элементе фазового пространства 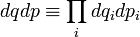 (с точкой q, p внутри) дается формулой:
(с точкой q, p внутри) дается формулой:Функцию
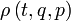 называют полной функцией статистического распределения (или просто функцией распределения). Фактически она представляет из себя плотность изображающих точек в фазовом пространстве. Функция
называют полной функцией статистического распределения (или просто функцией распределения). Фактически она представляет из себя плотность изображающих точек в фазовом пространстве. Функция 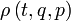 удовлетворяет условию нормировки
удовлетворяет условию нормировкипричем интеграл берется по всему фазовому пространству. В соответствующем механике случае система находится в определенном микроскопическом состоянии, то есть обладает заданными
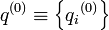 и
и 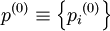 , и тогда
, и тогдагде
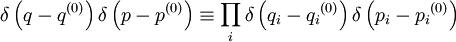 (δ - функция Дирака). Помимо самих вероятностей различных микроскопических состояний, функция
(δ - функция Дирака). Помимо самих вероятностей различных микроскопических состояний, функция 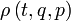 позволяет найти среднее статистическое значение любой физической величины
позволяет найти среднее статистическое значение любой физической величины 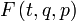 – функции фазовых переменных q и p:
– функции фазовых переменных q и p:где «крышечка» означает зависимость от фазовых переменных, а скобка – статистическое усреднение. Разобьем систему на малые, но макроскопические подсистемы. Можно утверждать о статистической независимости таких подсистем вследствие их слабого взаимодействия с окружением (во взаимодействии с окружением принимают участие лишь частицы, близкие к границе подсистемы; в случае макроскопичности подсистемы их число мало по сравнению с полным числом ее частиц). Статистическая независимость подсистем приводит к следующему результату для функции распределения
Индекс n относится к n-й подсистеме. Каждую из функций
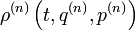 можно считать нормированной в соответствии с условием (2). При этом автоматически будет нормирована и функция ρ. Понятие о статистической независимости является приближенным. Приближенным в свою очередь является и равенство (3): оно не учитывает корреляции частиц, принадлежащих различным подсистемам. Существенно, однако, что в обычных физических условиях корреляции быстро ослабевают по мере удаления частиц (или групп частиц) друг от друга. Для системы существует характерный параметр – радиус корреляций, вне которого частицы ведут себя статистически независимо. В подсистемах макроскопических размеров подавляющее число частиц одной подсистемы лежит вне радиуса корреляций от частиц другой, и по отношению к этим частицам равенство (3) справедливо.
можно считать нормированной в соответствии с условием (2). При этом автоматически будет нормирована и функция ρ. Понятие о статистической независимости является приближенным. Приближенным в свою очередь является и равенство (3): оно не учитывает корреляции частиц, принадлежащих различным подсистемам. Существенно, однако, что в обычных физических условиях корреляции быстро ослабевают по мере удаления частиц (или групп частиц) друг от друга. Для системы существует характерный параметр – радиус корреляций, вне которого частицы ведут себя статистически независимо. В подсистемах макроскопических размеров подавляющее число частиц одной подсистемы лежит вне радиуса корреляций от частиц другой, и по отношению к этим частицам равенство (3) справедливо.Математически задание полной функции распределения
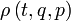 равносильно заданию бесконечного числа независимых величин – ее значений на континууме точек фазового пространства колоссальной размерности 2d (для макроскопических систем d ~ NA, где NA – число Авогадро).
равносильно заданию бесконечного числа независимых величин – ее значений на континууме точек фазового пространства колоссальной размерности 2d (для макроскопических систем d ~ NA, где NA – число Авогадро).В более реальном случае неполного измерения становятся известны вероятности значений или даже средние значения лишь некоторых физических величин
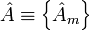 . Число их обычно бывает много меньше размерности фазового пространства системы. Функция распределения вероятностей
. Число их обычно бывает много меньше размерности фазового пространства системы. Функция распределения вероятностей 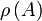 значений A дается равенством
значений A дается равенствомгде
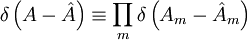 . Функция распределения
. Функция распределения 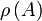 может быть названа неполной. Очевидно, она позволяет найти вероятности значений лишь физических величин
может быть названа неполной. Очевидно, она позволяет найти вероятности значений лишь физических величин 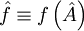 , зависимость которых от фазовых переменных осуществляется через
, зависимость которых от фазовых переменных осуществляется через 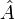 . Для таких же величин она позволяет найти и средние значения:
. Для таких же величин она позволяет найти и средние значения:где
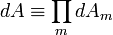 и интегрирование ведется по всем возможным значениям A. Конечно, средние значения
и интегрирование ведется по всем возможным значениям A. Конечно, средние значения 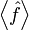 величин
величин 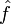 можно было бы найти с помощью полной функции распределения
можно было бы найти с помощью полной функции распределения 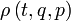 , если бы она была известна. Для функции
, если бы она была известна. Для функции 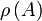 так же, как и для полной функции распределения, справедливо условие нормировки:
так же, как и для полной функции распределения, справедливо условие нормировки:Описание системы с помощью функции
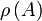 называется неполным описанием. Конкретными примерами служат описание с помощью функции распределения координат и импульсов отдельных частиц системы или описание с помощью средних значений масс, импульсов и энергий отдельных подсистем всей системы.
называется неполным описанием. Конкретными примерами служат описание с помощью функции распределения координат и импульсов отдельных частиц системы или описание с помощью средних значений масс, импульсов и энергий отдельных подсистем всей системы.Временная эволюция функции распределения подчиняется уравнению Лиувилля
где
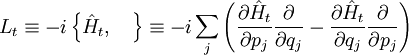 – оператор Лиувилля, действующий в пространстве фазовых функций,
– оператор Лиувилля, действующий в пространстве фазовых функций, 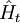 – функция Гамильтона системы. В случае, когда оператор Лиувилля не зависит от времени (Lt = L), решение уравнения (4) имеет вид
– функция Гамильтона системы. В случае, когда оператор Лиувилля не зависит от времени (Lt = L), решение уравнения (4) имеет видЧтобы использовать (5) для фактического построения решения, нужно знать собственные функции
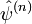 и собственные значения L(n) оператора L. Пользуясь полнотой и ортонормированностью
и собственные значения L(n) оператора L. Пользуясь полнотой и ортонормированностью 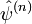 , напишем
, напишем 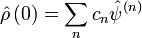 , где
, где 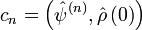 (спектр предполагается дискретным). В итоге получим
(спектр предполагается дискретным). В итоге получимСм также
- Частичная функция распределения
Литература
- Гиббс Дж. В. «Основные принципы статистической механики» — М. — Л., 1946. // Переиздано: Изд-во «Регулярная и хаотическая динамика», 2002. - 204 с. ISBN 5-93972-127-3.
- Балеску Р. Равновесная и неравновесная статистическая механика. В двух томах. — М.: Мир, 1978.
- Березин Ф. А. Лекции по статистической физике. — Москва–Ижевск: Институт. компьютерных исследований, 2002. - 192с. (2-ое изд, испр. Изд-во: МЦНМО, 2008. - 200 с. ISBN 978-5-94057-352-4)
- Боголюбов Н. Н. Проблемы динамической теории в статистической физике. — М.— Л.: ОГИЗ. Гостехиздат, 1946.
- Боголюбов Н. Н. Избранные труды по статистической физике. — М.: Изд-во МГУ, 1979.
- Боголюбов Н. Н. Собрание научных трудов. В 12 томах. Т. 5: «Неравновесная статистическая механика, 1939—1980». — М.: Наука, 2006. ISBN 5020341428.
- Власов А. А. Нелокальная статистическая механика. — М.: Наука, 1978.
- Зубарев Д. Н., Морозов В. Г., Репке Г. Статистическая механика неравновесных процессов. Том 1. — М.: ФИЗМАТЛИТ, 2002. — 432с. ISBN 5-9221-0211-7, ISBN 5-9221-0210-9.
- Пригожин И. Неравновесная статистическая механика. — Изд-во: Едиториал УРСС, 2005. - 312 с. ISBN 5-354-01004-7
- Хинчин А. Я. Математические основания статистической механики. — Изд-во: Регулярная и хаотическая динамика, 2003. - 128с. ISBN 5-93972-273-3
- Рюэль Д. Статистическая механика. Строгие результаты. — М.: Мир, 1971. - 368с.
- Крылов Н. С. Работы по обоснованию статистической физики. — М.-Л.: Из-во АН СССР, 1950.
- Кубо Р. Статистическая механика. — М.: Мир, 1967.
- Ландау, Л. Д., Лифшиц, Е. М. Статистическая физика. Часть 1. — («Теоретическая физика», том V).
- Терлецкий Я. П. Статистическая физика. (2-е изд.). — М.: Высшая школа, 1973.
- Уленбек Дж., Форд Дж. Лекции по статистической механике. — М.: Мир, 1965.]
- Хуанг К. Статистическая механика. — М.: Мир, 1966.
Wikimedia Foundation. 2010.