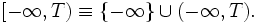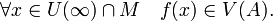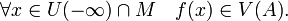- Пределы функции на бесконечности
-
 График функции, предел которой при аргументе, стремящемся к бесконечности, равен L.
График функции, предел которой при аргументе, стремящемся к бесконечности, равен L.Преде́л фу́нкции — одно из основных понятий математического анализа. Функция f(x) имеет предел A в точке x0, если для всех значений x, достаточно близких к x0, значение f(x) близко к A.
Содержание
Определения
- Пусть дана функция
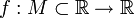 ,
, 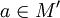 — предельная точка множества M,
— предельная точка множества M, 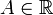 .
.
- (определение в терминах «ε−δ») Пусть
- (окрестностное определение по Коши) Пусть для любой окрестности V(A) точки A существует проколотая окрестность
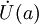 точки a такая, что образ этой окрестности
точки a такая, что образ этой окрестности 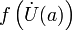 лежит в V(A):
лежит в V(A):
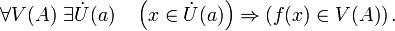
- Фундаментальное обоснование данного определения предела см. в статье Предел вдоль фильтра.
- (определение по Гейне)
- Будем называть
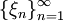 последовательностью Гейне, если
последовательностью Гейне, если
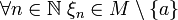
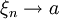 при
при 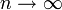 .
.
- Будем называть
- Пусть для любой последовательности Гейне имеем предел последовательности:
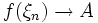 при
при 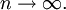
- (определение в терминах «ε−δ») Пусть
- Тогда A называется пределом функции f при x, стремящемся к a
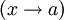 .
.
Все данные выше определения предела функции в точке эквивалентны.
Обозначения
Если предел функции f при
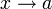 существует и равен A, пишут
существует и равен A, пишутСвойства пределов числовых функций
Пусть даны функции
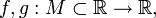 и
и 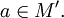 Тогда
Тогда- Предел
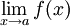 единственен, то есть
единственен, то есть
Доказательство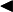 Доказательство методом от противного. Пусть существует
Доказательство методом от противного. Пусть существует 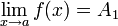 и
и 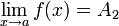 и
и 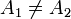 . Предположим A1 < A2. Возьмём
. Предположим A1 < A2. Возьмём 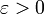 , такое что
, такое что 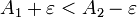 , т.е.
, т.е. 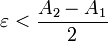 .
.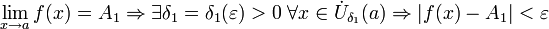 , т.е.
, т.е. 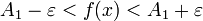 .
.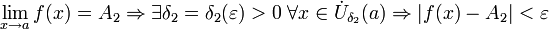 , т.е.
, т.е. 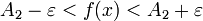 .
.Тогда получаем
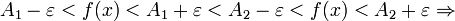 Противоречие. Значит предел единственный.
Противоречие. Значит предел единственный. 
- Сходящаяся функция локально сохраняет знак. Более общо,
- где
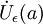 — проколотая окрестность точки a.
— проколотая окрестность точки a.
- В частности, функция, сходящаяся к положительному (отрицательному) пределу, остаётся положительной (отрицательной) в некоторой окрестности предельной точки:
- Сходящаяся функция локально ограничена в окрестности предельной точки:
- Операция взятия предела сохраняет нестрогие неравенства.
- Предел суммы равен сумме пределов:
- Предел разности равен разности пределов:
- Предел произведения равен произведению пределов:
- Предел частного равен частному пределов.
Вариации и обобщения
- Односторонний предел — левый или правый предел в точке.
- Предел вдоль фильтра.
Пределы на бесконечности
Предел функции на бесконечности описывает поведение значения данной функции, когда её аргумент становится бесконечно большим (по абсолютной величине).
- Определения, аналогичные «ε−δ»
- Пусть задана числовая функция с неограниченной сверху областью определения, то есть
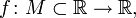 и
и 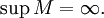 Число
Число 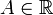 называется пределом функции f при
называется пределом функции f при 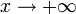 (предел в плюс бесконечности), если
(предел в плюс бесконечности), если
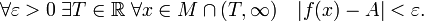
- Пишут:
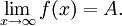
- Аналогично пусть
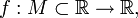 и
и 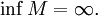 Число
Число 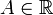 называется пределом функции f при
называется пределом функции f при 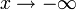 (предел в минус бесконечности), если
(предел в минус бесконечности), если
- Пишут:
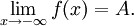
- Если пределы в
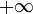 и
и 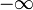 существуют и равны, то говорят что функция имеет предел в бесконечности:
существуют и равны, то говорят что функция имеет предел в бесконечности:
- Число
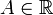 называется пределом функции f при
называется пределом функции f при 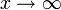 (предел в бесконечности), если
(предел в бесконечности), если 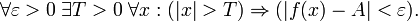
- Число
- Окрестностное определение
Расширенная числовая прямая
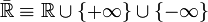 становится топологическим пространством, если её снабдить естественной топологией, определив окрестности бесконечных точек следующим образом:
становится топологическим пространством, если её снабдить естественной топологией, определив окрестности бесконечных точек следующим образом:- Окрестностью точки
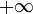 является любой интервал
является любой интервал
- Окрестностью точки
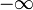 является любой интервал
является любой интервал
Пределы функции на бесконечностях тогда можно определить как обычные пределы на топологическом пространстве.
- Число A называется пределом функции f при x, стремящемся к плюс бесконечности, если для любой окрестности V(A) существует окрестность
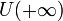 такая, что
такая, что
- Число A называется пределом функции f при x, стремящемся к минус бесконечности, если для любой окрестности V(A) существует окрестность
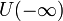 такая, что
такая, что
- Если отождествить точки
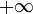 и
и 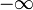 , то окрестности бесконечности будут иметь вид, например,
, то окрестности бесконечности будут иметь вид, например, 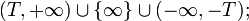
- Число A называется пределом функции f при x, стремящемся к бесконечности, если для любой окрестности V(A) существует окрестность
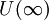 такая, что
такая, что
См. также
Ссылки
Литература
- Математический энциклопедический словарь / Под ред. Ю. В. Прохорова. — М.: Советская энциклопедия, 1988. — С. 482—483. — 847 с.
- Пусть дана функция
Wikimedia Foundation. 2010.

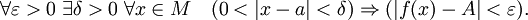
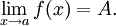
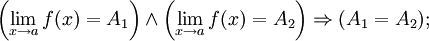
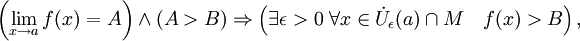
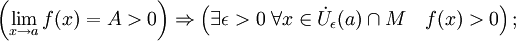
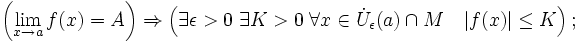
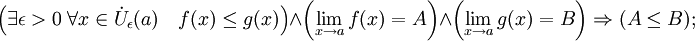
![\left( \lim\limits_{x \to a} f(x) = A \right) \wedge \left( \lim\limits_{x \to a} g(x) = B \right) \Rightarrow \left( \lim\limits_{x \to a} \bigl[f(x)+g(x)\bigr] = A+B \right);](/pictures/wiki/files/57/95e0b04e48ae4f91790a30e707ff58d3.png)
![\left( \lim\limits_{x \to a} f(x) = A \right) \wedge \left( \lim\limits_{x \to a} g(x) = B \right) \Rightarrow \left( \lim\limits_{x \to a} \bigl[f(x)-g(x)\bigr] = A-B \right);](/pictures/wiki/files/49/10d7a60c276fe14d2b7d12332ad4fc9d.png)
![\left( \lim\limits_{x \to a} f(x) = A \right) \wedge \left( \lim\limits_{x \to a} g(x) = B \right) \Rightarrow \left( \lim\limits_{x \to a} \bigl[f(x)\cdot g(x)\bigr] = A\cdot B \right);](/pictures/wiki/files/55/7c1b68990fe95846eea662e9686e18ff.png)
![\left( \lim\limits_{x \to a} f(x) = A \right) \wedge \left( \lim\limits_{x \to a} g(x) = B \neq 0 \right) \Rightarrow \left( \lim\limits_{x \to a} \left[\frac{f(x)}{g(x)}\right] = \frac{A}{B}\right).](/pictures/wiki/files/55/7512622b5e786b5d649076d42b1bdae2.png)
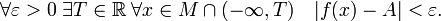
![(T,+\infty] \equiv (T,+\infty) \cup \{+\infty\};](/pictures/wiki/files/49/108e023eb85f2700cab2ff61a58b6568.png)