- Равномеpно темперированный звукоряд
-
Темпери́рованный строй — строй, при котором каждая октава делится на набор одинаковых ступеней. Чаще всего деление происходит на двенадцать ступеней, отстоящих друг от друга на расстоянии хроматического полутона (
![1:\sqrt[12]{2}](/pictures/wiki/files/51/391b450d4863bac50ff999be9542463e.png) ). Такой строй господствует в западной музыке с XIX века.
). Такой строй господствует в западной музыке с XIX века.Существуют и другие темперированные строи, или равномерные темперации (РТ). В восточной музыке встречается 24-тоновая РТ (24-тРТ). Индийская музыка основана на строях, близких к 22-тРТ. Некоторая музыка была написана в 19-тРТ, 31-тРТ и даже 53-тРТ. Когда же говорят просто «равномерная темперация», без уточнений, это понимается, как 12-тРТ.
Равномерные темперации могут также делить иной интервал, не только октаву, на целое число равных ступеней. Чтобы избежать неясности, предложен термин «равные деления октавы», или РДО. Согласно этой системе 12-тРТ переименовывается в 12РДО, 19-тРТ в 19РДО, и так далее.
История
12-ступенный равномерно темперированный строй возник в обстановке поисков музыкальными теоретиками идеального строя. Исторически предшествующий натуральный строй имел ряд недостатков, которые исчезали с введением равномерной темперации. Исчезала комма. Появилась возможность сочинять музыку в разных тональностях, не боясь волчьих квинт.
У нового строя было много оппонентов. Новый строй нарушал строгую пропорцию интервалов, как следствие, в аккордах начали появляться небольшие биения. В глазах многих теоретиков это было посягательством на чистоту музыки. Андреас Веркмейстер утверждал, что в новом строе все тональности становились однообразными и симметричными, в то время как в старых строях из-за неравномерности темперации каждая тональность имела своё неповторимое звучание.
В качестве одного из аргументов дискуссии интересен «Хорошо темперированный клавир» И. С. Баха, сборник прелюдий и фуг во всех возможных тональностях.
Со временем равномерная темперация завоевала признание и стала фактическим стандартом.
Вычисление частот звуков
Можно математически вычислить частоты для всего звукоряда пользуясь формулой:
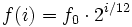 ,
,
Где f0 — частота камертона (например Ля 440 Hz), а i — количество полутонов в интервале от искомого звука к эталону f0. Последовательность вычисленных таким образом частот образует геометрическую прогрессию
Например, можно вычислить звук на тон (2 полутона) ниже от камертона Ля:
- i = − 2
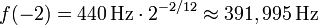
Получим соль. Если нам надо вычислить ноту соль, но на октаву выше (12 полутонов)
- i = 12 − 2 = 10
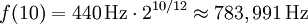
Частоты двух полученных нот Соль отличаются в два раза, что дает чистую октаву. Преимущества равномерной темперации также в том, что можно произвольно транспонировать пьесу на любой интервал вверх или вниз, и она не потеряет гармонии.
Сравнение с натуральным строем
Равномерно темперированный строй очень легко можно отобразить в виде измерения интервалов в центах
Тон C1 C# D Eb E F F# G G# A B H C2 Цент (музыка) 0 100 200 300 400 500 600 700 800 900 1000 1100 1200 Следующая таблица показывает отличия интервалов равномерно-темперированного ряда с натуральным
Интервал Равномерно темперированные интервалы Натуральные интервалы Разница в центах Прима ![\sqrt[12]{2^0} = 1 = 0\,\mathrm{Cent}](/pictures/wiki/files/55/7bfae1a0c2a7c3c3b71954c5ed38bbc2.png)
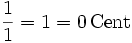
0 Малая секунда ![\sqrt[12]{2^1} = \sqrt[12]{2} \approx 1{,}059463 = 100\,\mathrm{Cent}](/pictures/wiki/files/53/569629309403474d4caf9cb70e547fae.png)
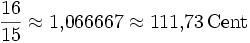
−11,73 Большая секунда ![\sqrt[12]{2^2} = \sqrt[6]{2} \approx 1{,}122462 = 200\,\mathrm{Cent}](/pictures/wiki/files/48/05b91071a9693f74e0f043bb002f3c53.png)
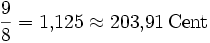
−3,91 Малая терция ![\sqrt[12]{2^3} = \sqrt[4]{2} \approx 1{,}189207 = 300\,\mathrm{Cent}](/pictures/wiki/files/54/650c85c1a9cbfcd9e62c8a25dc58d643.png)
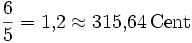
−15,64 Большая терция ![\sqrt[12]{2^4} = \sqrt[3]{2} \approx 1{,}259921 = 400\,\mathrm{Cent}](/pictures/wiki/files/49/1a9b5ef2e324b67870c308ff08439f40.png)
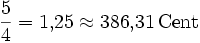
13,69 Кварта ![\sqrt[12]{2^5} = \sqrt[12]{32} \approx 1{,}334840 = 500\,\mathrm{Cent}](/pictures/wiki/files/99/cbb5065aec9048e743958300d7a1a25a.png)
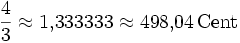
1,96 Тритон ![\sqrt[12]{2^6} = \sqrt{2} \approx 1{,}414214 = 600\,\mathrm{Cent}](/pictures/wiki/files/99/cd7c42b05fd8ec05c2a9275f3b3c2898.png)
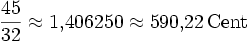
9,78 Квинта ![\sqrt[12]{2^7} = \sqrt[12]{128} \approx 1{,}498307 = 700\,\mathrm{Cent}](/pictures/wiki/files/52/4660112ae7052372f5a083e8e5853b06.png)
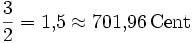
−1,96 Малая секста ![\sqrt[12]{2^8} = \sqrt[3]{4} \approx 1{,}587401 = 800\,\mathrm{Cent}](/pictures/wiki/files/99/cb69e8650aaace47033812ba87ae9904.png)
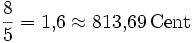
−13,69 Большая секста ![\sqrt[12]{2^9} = \sqrt[4]{8} \approx 1{,}681793 = 900\,\mathrm{Cent}](/pictures/wiki/files/54/618e524a0b4a474f61d131908916557e.png)
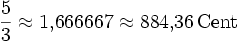
15,64 Малая септима ![\sqrt[12]{2^{10}} = \sqrt[6]{32} \approx 1{,}781797 = 1000\,\mathrm{Cent}](/pictures/wiki/files/54/6462998982b96de746d0ba522b458e1b.png)
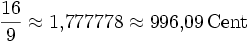
3,91 Большая септима ![\sqrt[12]{2^{11}} = \sqrt[12]{2048} \approx 1{,}887749 = 1100\,\mathrm{Cent}](/pictures/wiki/files/49/160897d9f54dd446c52eea750bfbf1d1.png)
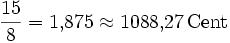
11,73 Октава ![\sqrt[12]{2^{12}} = 2 = 1200\,\mathrm{Cent}](/pictures/wiki/files/49/1ca19e5a24a53a0b5ed1349f91a262f3.png)
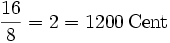
0 Музыкальный строй Пифагорейский строй | Натуральный строй | Среднетоновый строй | Равномерно темперированный строй
Wikimedia Foundation. 2010.
