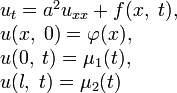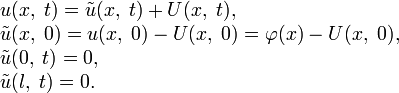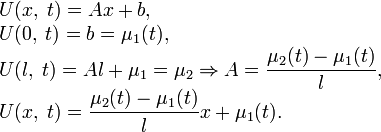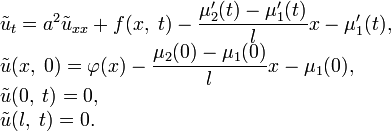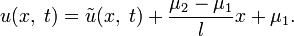- Принцип максимума (уравнение теплопроводности)
-
Механика сплошных сред 
Сплошная среда Классическая механика Закон сохранения массы · Закон сохранения импульса Теория упругости Напряжение · Тензор · Твёрдые тела · Упругость · Пластичность · Закон Гука · Реология · Вязкоэластичность Гидродинамика Жидкость · Гидростатика · Гидродинамика · Вязкость · Ньютоновская жидкость · Неньютоновская жидкость · Поверхностное натяжение Основные уравнения Уравнение непрерывности · Уравнение Эйлера · Уравнения Навье — Стокса · Уравнение диффузии · Закон Гука Известные учёные Ньютон · Гук
Бернулли · Эйлер · Коши · Стокс · НавьеУравнение диффузии или уравнение теплопроводности представляет собой частный вид дифференциального уравнения в частных производных. Бывает нестационарным и стационарным.
Математически уравнение диффузии и уравнение теплопроводности не различаются, и применение того или иного названия ограничено только конкретным приложением, причем второе представляется более частным, так как можно говорить, что в этом случае речь идет о диффузии тепловой энергии.
В смысле интерпретации при решении уравнения диффузии речь идет о нахождении зависимости концентрации вещества (или иных объектов) от пространственных координат и времени, причем задан коэффициент (в общем случае также зависящий от пространственных координат и времени), характеризующий проницаемость среды для диффузии. При решении уравнения теплопроводности речь идет о нахождении зависимости температуры среды от пространственных координат и времени, причем задана теплоемкость и теплопроводность среды (также в общем случае неоднородной).
Физически в том и другом случае предполагается отсутствие или пренебрежимость макроскопических потоков вещества. Таковы физические рамки применимости этих уравнений. Также, представляя непрерывный предел указанных задач (то есть не более, чем некоторое приближение), уравнение диффузии и теплопроводности в общем не описывают статистических флуктуаций и процессов, близких по масштабу к длине и времени свободного пробега, также весьма сильно отклоняясь от предполагаемого точного решения задачи в том, что касается корреляций на расстояниях, сравнимых (и больших) с расстояниями, проходимыми звуком (или свободными от сопротивления среды частицами при их характерных скоростях) в данной среде за рассматриваемое время.
Это в подавляющей части случаев сразу же означает и то, что уравнения диффузии и теплопроводности по области применимости далеки от тех областей, где становятся существенными квантовые эффекты или конечность скорости света, то есть в подавляющей части случаев не только по своему выводу, но и принципиально, ограничиваются областью классической ньютоновской физики.
- Ближайшим формальным, а во многом и содержательным, аналогом уравнения диффузии является уравнение Шрёдингера, отличающееся от уравнения диффузии множителем мнимая единица перед производной по времени. Многие теоремы о решении уравнения Шрёдингера и даже некоторые виды формальной записи его решений прямо аналогичны соответствующим теоремам об уравнении диффузии и его решениях, однако качественно их решения различаются очень сильно.
Содержание
Нестационарное уравнение
Нестационарное уравнение диффузии классифицируется как параболическое дифференциальное уравнение. Оно описывает распространение растворяемого вещества вследствие диффузии или перераспределение температуры тела в результате теплопроводности.
Одномерный случай
В случае одномерного диффузионного процесса с коэффициентом диффузии (теплопроводности) D уравнение имеет вид:
При постоянном D приобретает вид:
где
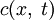 — концентрация диффундирующего вещества, a
— концентрация диффундирующего вещества, a 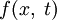 — функция, описывающая источники вещества (тепла).
— функция, описывающая источники вещества (тепла).Трёхмерный случай
В трёхмерном случае уравнение приобретает вид:
где
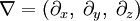 — оператор набла, а
— оператор набла, а 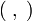 — скалярное произведение. Оно также может быть записано как
— скалярное произведение. Оно также может быть записано кака при постоянном D приобретает вид:
где
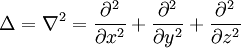 — оператор Лапласа.
— оператор Лапласа.n-мерный случай
n-мерный случай — прямое обобщение приведенного выше, только под оператором набла, градиентом и дивергенцией, а также под оператором Лапласа надо понимать n-мерные версии соответствующих операторов:
Это касается и двумерного случая n = 2.
Мотивировка
A.
Обычно уравнение диффузии возникает из эмпирического (или как-то теоретически полученного) уравнения, утверждающего пропорциональность потока вещества (или тепловой энергии) разности концентраций (температур) областей, разделённых тонким слоем вещества заданной проницаемости, характеризуемой коэффициентом диффузии (или теплопроводности):
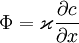 (одномерный случай),
(одномерный случай),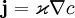 (для любой размерности),
(для любой размерности),
в сочетании с уравнением непрерывности, выражающим сохранение вещества (или энергии):
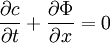 (одномерный случай),
(одномерный случай),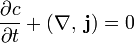 (для любой размерности),
(для любой размерности),
с учетом в случае уравнения теплопроводности ещё теплоёмкости (температура = плотность энергия / удельная теплоемкость).
- Здесь источник вещества (энергии) в правой части опущен, но он, конечно же, может быть легко туда помещён, если в задаче есть приток (отток) вещества (энергии).
B.
Кроме того, оно естественно возникает как непрерывный предел аналогичного разностного уравнения, возникающего в свою очередь при рассмотрении задачи о случайном блуждании на дискретной решётке (одномерной или n-мерной). (Это простейшая модель; в более сложных моделях случайных блужданий уравнение диффузии также возникает в непрерывном пределе). Простейшей интерпретацией функции c в этом случае служит количество (или концентрация) частиц в данной точке (или вблизи неё), причём каждая частица движется независимо от остальных без памяти (инерции) своего прошлого (в несколько более сложном случае — с ограниченной по времени памятью).
Решение
В одномерном случае фундаментальное решение однородного уравнения с постоянным — не зависящем от x и t — D (при начальном условии, выражаемом дельта-функцией
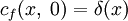 и граничном условии
и граничном условии 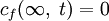 ) есть
) естьВ этом случае
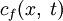 можно интерпретировать как плотность вероятности того, что одна частица, находившаяся в начальный момент времени в исходном пункте, через время t перейдёт в пункт с координатой x. То же самое — с точностью до множителя, равного количеству диффундирующих частиц — относится к их концентрации, при условии отсутствия или пренебрежимости взаимодействия диффундирующих частиц между собой. Тогда (при таких начальных условиях) средний квадрат удаления диффундирующих частиц (или соответствующая характеристика распределения температуры) от начальной точки
можно интерпретировать как плотность вероятности того, что одна частица, находившаяся в начальный момент времени в исходном пункте, через время t перейдёт в пункт с координатой x. То же самое — с точностью до множителя, равного количеству диффундирующих частиц — относится к их концентрации, при условии отсутствия или пренебрежимости взаимодействия диффундирующих частиц между собой. Тогда (при таких начальных условиях) средний квадрат удаления диффундирующих частиц (или соответствующая характеристика распределения температуры) от начальной точки
В случае произвольного начального распределения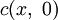 общее решение уравнения диффузии представляется в интегральном виде как свёртка:
общее решение уравнения диффузии представляется в интегральном виде как свёртка:Физические замечания
Так как приближение, реализуемое уравнениями диффузии и теплопроводности, принципиально ограничивается областью низких скоростей и макроскопических масштабов (см. выше), то неудивительно, что их фундаментальное решение на больших расстояниях ведёт себя не слишком реалистично, формально допуская бесконечное распространение воздействия в пространстве за конечное время; надо при этом заметить, что величина этого воздействия так быстро убывает с расстоянием, что этот эффект как правило в принципе ненаблюдаем (например, речь идёт о концентрациях много меньше единицы).
Впрочем, если речь идёт о ситуациях, когда могут быть экспериментально измерены столь маленькие концентрации, и это для нас существенно, нужно пользоваться по меньшей мере не дифференциальным, а разностным уравнением диффузии, а лучше — и более подробными микроскопической физической и статистической моделями, чтобы получить более адекватное представление о реальности в этих случаях.
Стационарное уравнение
В случае, когда ставится задача по нахождению установившегося распределения плотности или температуры (например, в случае, когда распределение источников не зависит от времени), из нестационарного уравнения выбрасывают члены уравнения, связанные с временем. Тогда получается стационарное уравнение теплопроводности, относящееся к классу эллиптических уравнений. Его общий вид:
- При D, не зависящем от
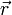 , стационарное уравнение диффузии становится уравнением Пуассона (неоднородное), или уравнением Лапласа (однородное, то есть при f = 0):
, стационарное уравнение диффузии становится уравнением Пуассона (неоднородное), или уравнением Лапласа (однородное, то есть при f = 0):
Постановка краевых задач
- Задача с начальными условиями (задача Коши) о распределении температуры на бесконечной прямой
Если рассматривать процесс теплопроводности в очень длинном стержне, то в течении небольшого промежутка времени влияние температур на границах практически отсутствует, и температура на рассматриваемом участке зависит лишь от начального распределения температур.
Найти решение уравнения теплопроводности в области
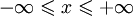 и
и 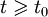 , удовлетворяющее условию
, удовлетворяющее условию 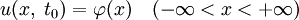 , где
, где 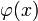 — заданная функция.
— заданная функция.- Первая краевая задача для полубесконечного стержня
Если интересующий нас участок стержня находится вблизи одного конца и значительно удалён от другого, то мы приходим к краевой задаче, в которой учитывается влияние лишь одного из краевых условий.
Найти решение уравнения теплопроводности в области
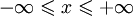 и
и 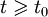 , удовлетворяющее условиям
, удовлетворяющее условиямгде
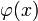 и μ(t) — заданнные функции.
и μ(t) — заданнные функции.- Краевая задача без начальных условий
Если момент времени который нас интересует достаточно удалён от начального, то имеет смысл принебречь начальными условиями, поскольку их влияние на процесс с течением времени ослабевает. Таким образом, мы приходим к задаче, в которой заданы краевые условия и отсутствуют начальные.
Найти решение уравнения теплопроводности в области
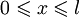 и
и 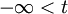 , удовлетворяющее условиям
, удовлетворяющее условиямгде μ1(t) и μ2(t) — заданнные функции.
- Краевые задачи для ограниченного стержня
Рассмотрим следущую краевую задачу:
 — уравнение теплопроводности.
— уравнение теплопроводности.
Если
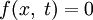 , то такое уравнение называют однородным, в противном случае — неоднородным.
, то такое уравнение называют однородным, в противном случае — неоднородным.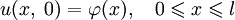 — начальное условие в момент времени t = 0, температура в точке x задается функцией
— начальное условие в момент времени t = 0, температура в точке x задается функцией 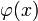 .
.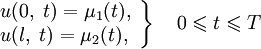 — краевые условия. Функции μ1(t) и μ2(t) задают значение температуры в граничных точка 0 и l в любой момент времени t.
— краевые условия. Функции μ1(t) и μ2(t) задают значение температуры в граничных точка 0 и l в любой момент времени t.
В зависимости от рода краевых условий, задачи для уравнения теплопроводности можно разбить на три типа. Рассмотрим общий случай (
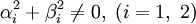 ).
).Если
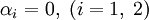 , то такое условие называют условием первого рода, если
, то такое условие называют условием первого рода, если 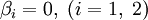 — второго рода, а если αi и βi отличны от нуля, то условием третьего рода. Отсюда получаем задачи для уравнения теплопроводности — первую, вторую и третью краевую.
— второго рода, а если αi и βi отличны от нуля, то условием третьего рода. Отсюда получаем задачи для уравнения теплопроводности — первую, вторую и третью краевую.Способы решения уравнений теплопроводности
Метод разделения переменных
Однородное уравнение теплопроводности с однородными граничными условиями
Рассмотрим следующую задачу
Требуется найти функцию
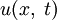 для
для 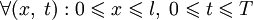 .
.Представим искомую функцию в виде произведения
Затем предполагаемую форму решения подставим в исходное уравнение, получим
- X(x)T'(t) = a2X''(x)T(t).
Разделим выражение на a2X(x)T(t):
Так как в левой части уравнения у нас находится функция зависящая только от t, а в правой — только от x, то, фиксируя любое значение x в правой части, получаем, что для любого t значение левой части уравнения постоянно. Таким же образом можно убедиться, что и правая часть постоянна, то есть равна некой константе − λ (минус взят для удобства). Таким образом, мы получаем два обыкновенных линейных дифференциальных уравнения:
Обратим внимание на граничные условия исходной задачи и подставим в них предполагаемый вид уравнения, получим:
откуда X(0) = X(l) = 0 (
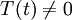 , так как в противном случае мы имели бы решение
, так как в противном случае мы имели бы решение 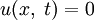 , а мы ищем только нетривиальные решения).
, а мы ищем только нетривиальные решения).С учетом полученных граничных условий мы получаем задачу Штурма — Лиувилля:
Её решение сводится к решению линейного дифференциального уравнения и рассмотрению трёх случаев:
- λ < 0.
- В этом случае общий вид решения будет следующим:
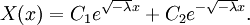
- Подставив граничные условия, мы убедимся, что решение будет
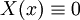 , а мы ищем только нетривиальные решения, следовательно, этот случай не подходит.
, а мы ищем только нетривиальные решения, следовательно, этот случай не подходит.
- λ = 0.
- Общий вид решения
- X(x) = C1x + C2.
- Несложно убедиться, что этот вариант нам также не подходит.
- λ > 0.
- Общий вид решения
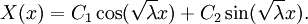
- Подставим граничные условия:
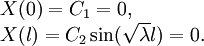
- Так как мы ищем только нетривиальные решения, C2 = 0 нам не подходит, следовательно
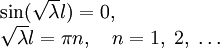
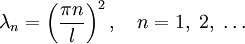
- Отсюда
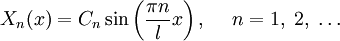
C учетом найденных λ, выведем общее решение линейного дифференциального уравнения
Должен получиться ответ
Теперь всё готово для того, чтобы записать решение исходной задачи:
В результате у нас получилось бесконечное количество частных решений уравнения. Все эти частные решения линейно независимы, то есть линейная комбинация любого количества решений равна нулю, только если все коэффициенты при них равны нулю. Поэтому логично предположить, что суммируя все частные решения по n от единицы до бесконечности, мы получим общее решение исходной задачи.
Осталось определить значение константы C (зависящей от n) из начального условия
Для того, чтобы определить значение Cn, необходимо разложить функцию
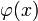 в ряд Фурье:
в ряд Фурье:Получаем:
Откуда общее решение:
В курсе математической физики доказывается, что полученный ряд удовлетворяет всем условиям данной задачи, то есть функция
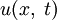 дифференцируема (и ряд сходится равномерно), удовлетворяет уравнению в области определения и непрерывна в точках границы этой области.
дифференцируема (и ряд сходится равномерно), удовлетворяет уравнению в области определения и непрерывна в точках границы этой области.Неоднородное уравнение теплопроводности с однородными граничными условиями
Рассмотрим способ решения неоднородного уравнения:
Пусть
Тогда, пользуясь очевидным соотношением
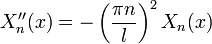 , перепишем исходное уравнение как:
, перепишем исходное уравнение как:Решим последнее линейное неоднородное уравнение методом вариации постоянной. Сначала найдём общее решение однородного линейного уравнения
В общем решении заменим постоянную D на переменную D(t) и подставим в исходное уравнение.
Из начального условия получаем:
С учетом условия для T, получаем
Так как
то Fn(t), очевидно, является коэффициентом ряда Фурье, и равен
В результате, общая формула такова:
Общая первая краевая задача
Во многих случаях удаётся решить уравнение теплопроводности с неоднородными краевыми и начальным условиями
с помощью методов, описанных выше и следующего несложного приёма. Представим искомую функцию в виде суммы:
Найдём функцию
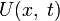 :
:Таким образом, исходная задача свелась к следующей:
После того, как мы найдём функцию
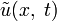 , искомую функцию найдём по формуле
, искомую функцию найдём по формулеПринцип максимума
Пусть функция
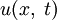 в пространстве
в пространстве ![D\times[0,\;T],\;D\in\R^n](/pictures/wiki/files/51/3d3186ed8568ed770a75bd284a587574.png) , удовлетворяет однородному уравнению теплопроводности
, удовлетворяет однородному уравнению теплопроводности 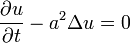 , причем D — ограниченная область. Принцип максимума утверждает, что функция
, причем D — ограниченная область. Принцип максимума утверждает, что функция 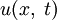 может принимать экстремальные значения либо в начальный момент времени, либо на границе области D.
может принимать экстремальные значения либо в начальный момент времени, либо на границе области D.
Wikimedia Foundation. 2010.

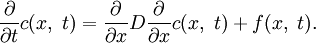
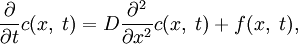
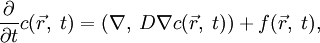
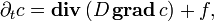
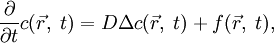
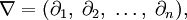
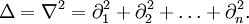
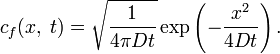
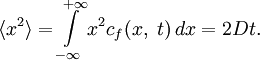
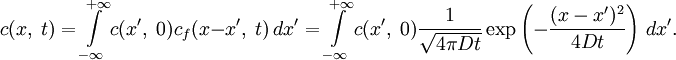
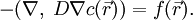
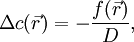
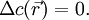
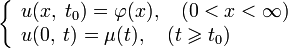
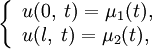
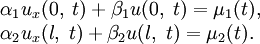
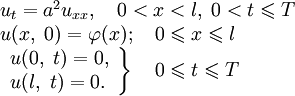
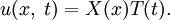
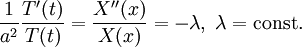
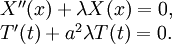
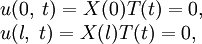
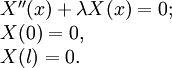

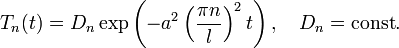
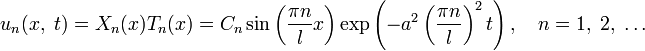
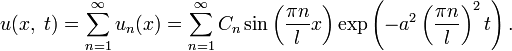
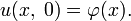
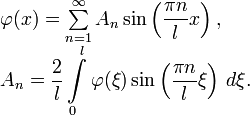
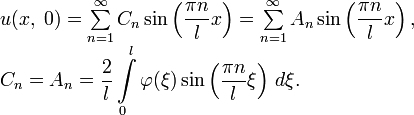
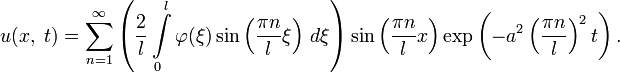
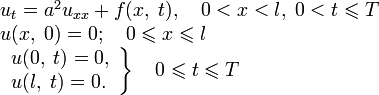
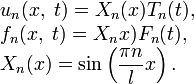
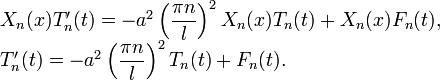
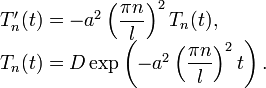
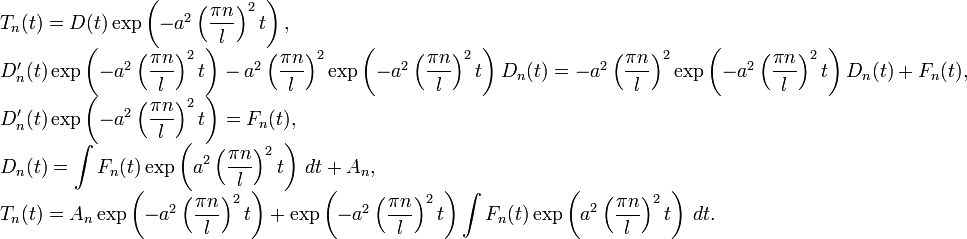
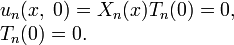
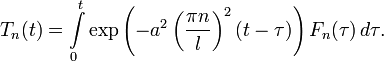
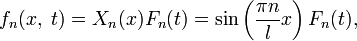
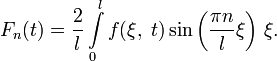
![u(x,\;t)=\sum\limits_{n=1}^\infty X_n(x)T_n(t)=\sum\limits_{n=1}^\infty \left[\int\limits_0^t \exp\left(-a^2\left(\frac{\pi n}{l}\right)^2 (t-\tau)\right)\left\{\frac{2}{l}\int\limits_0^l f(\xi,\;\tau)\sin\left(\frac{\pi n}{l}\xi\right)\,d\xi\right\}\,d\tau\right]\sin\left(\frac{\pi n}{l}x\right).](/pictures/wiki/files/100/d92af4927f913473ca7d5f3d1e2b26c9.png)