Парадокс Банаха—Тарского

Шар можно «разбить» на куски и собрать из них два таких же шара.

Парадокс Банаха — Тарского, или парадокс удвоения шара, говорит, что трёхмерный шар равносоставлен двум своим копиям.

Два подмножества евклидова пространства называются равносоставленными, если одно можно разбить на конечное число «кусков» и составить из них второе. При этом для удвоения шара достаточно пяти кусков, но четырёх недостаточно.

Более точно, два множества A и B являются равносоставленными, если их можно представить как конечное объединение непересекающихся подмножеств 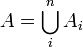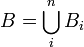$A=\bigcup_i ^nA_i$, $B=\bigcup_i^n B_i$ так, что для каждого i подмножество A_i конгруэнтно B_i.

Верен также более сильный вариант парадокса:

Любые два ограниченных подмножества евклидова пространства с непустой внутренностью являются равносоставленными.

Ввиду своей неправдоподобности, этот парадокс часто используется как довод против принятия аксиомы выбора, которая существенно используется при построении такого разбиения. Принятие подходящей альтернативной аксиомы позволяет доказать невозможность указанного разбиения, не оставляя места для этого парадокса.

Парадокс был открыт в 1926 году Стефаном Банахом и Альфредом Тарским. Очень похож на более ранний парадокс Хаусдорфа, и его доказательство основано на той же идее. Поэтому более правильно называть парадоксом Хаусдорфа — Банаха — Тарского.

Значение для теории меры

Разделяя шар на конечное число частей, мы интуитивно ожидаем, что, складывая эти части вместе, можно получить только сплошные фигуры, объём которых равен объёму исходного шара радиуса. Однако это справедливо только в случае, когда шар делится на части, имеющие объём. Суть парадокса заключается в том, что в трёхмерном пространстве существуют неизмеримые множества, которые не имеют объёма, если под объёмом мы понимаем то, что обладает свойством аддитивности, и предполагаем, что объёмы двух конгруэнтных множеств совпадают. Очевидно, что «куски» в таком разбиении не могут быть измеримыми (и невозможно осуществить такое разбиение какими-либо средствами на практике).

Для плоского круга аналогичная теорема неверна. Более того, Банах показал, что на плоскости понятие площади может быть продолжено на все ограниченные множества как конечно-аддитивная мера, инвариантная относительно движений; в частности, любое множество, равносоставленное кругу, имеет ту же площадь. Хаусдорф показал, что подобное сделать нельзя на двумерной сфере, и, следовательно, в трёхмерном пространстве, и парадокс Банаха — Тарского даёт этому наглядную иллюстрацию.

Тем не менее, некоторые парадоксальные разбиения возможны и на плоскости: круг можно разбить на конечное число кусков и составить из них квадрат равной площади.

Литература

• Это построение очень подробно описано в книге И. В. Ященко «Парадоксы теории множеств»
• Оригинальная статья Банаха и Тарского (на французском): «Sur la décomposition des ensembles de points en parties respectivement congruentes», Fundamenta Mathematicae, 6, (1924), 244—277.
• F. Hausdorff, Bemerkung über den Inhalt von Punktmengen Mathematische Annalen, vol 75. (1914) pp. 428—434.
• Секей Г. Парадоксы в теории вероятностей и математической статистике. Пер. с англ. — Москва-Ижевск: ИКИ, 2003. — 272 с.