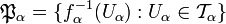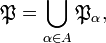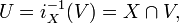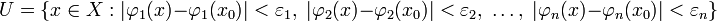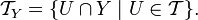- Относительная топология
-
Индуци́рованная или относи́тельная тополо́гия в общей топологии — это естественный способ задания топологии на подмножестве топологического пространства.
Основная конструкция индуцированной топологии. Пусть X — множество, и задано семейство отображений
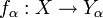 в топологические пространства Yα с топологией
в топологические пространства Yα с топологией 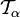 , где
, где 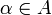 . Тогда каждое семейство множеств
. Тогда каждое семейство множествобразует некоторую топологию пространства X (выполнены все аксиомы топологического пространства!), причём в этой топологии отображение fα будет непрерывным.
Однако пространство X можно наделить структурой топологического пространства так, чтобы все эти отображения стали непрерывными одновременно. Для этого нужно построить её предбазу
по ней (с помощью конечных пересечений) — базу
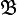 , а по базе построить полную топологию, которая называется топологией, индуцированной на X семейством отображений fα.
, а по базе построить полную топологию, которая называется топологией, индуцированной на X семейством отображений fα.Пример. Пусть X — подмножество пространства Y, имеющего топологию
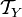 . Тогда определено отображение включения
. Тогда определено отображение включения 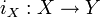 по формуле iX(x) = x. Оно индуцирует топологию на пространстве X. Открытыми в этой топологии являются те и только те подмножества U пространства X, которые представимы в виде:
по формуле iX(x) = x. Оно индуцирует топологию на пространстве X. Открытыми в этой топологии являются те и только те подмножества U пространства X, которые представимы в виде:где
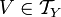 — открытое подмножество пространства Y. Такая топология называется топологией подпространства, а само X с такой топологией — топологическим подпространством пространства Y.
— открытое подмножество пространства Y. Такая топология называется топологией подпространства, а само X с такой топологией — топологическим подпространством пространства Y.Пример. Пусть Xα — любое семейство топологических пространств, и
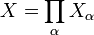 — их декартово произведение. Тогда определены отображения проекции
— их декартово произведение. Тогда определены отображения проекции 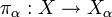 на каждую компоненту. С помощью процедуры, описанной выше, строится топология, относительно которой все эти проекции непрерывны. Эта топология называется тихоновской, а само пространство X с такой топологией — тихоновским произведением пространств Xα.
на каждую компоненту. С помощью процедуры, описанной выше, строится топология, относительно которой все эти проекции непрерывны. Эта топология называется тихоновской, а само пространство X с такой топологией — тихоновским произведением пространств Xα.Пример. Пусть X — векторное пространство над полем
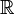 или
или 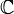 , и
, и 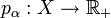 — произвольное семейство преднорм, которые одновременно могут обращаться в нуль только в нуле пространства X. Основная конструкция индуцирования применима, и в результате её пространство X наделяется локально-выпуклой топологией полинормированного пространства с (непрерывными) преднормами pα.
— произвольное семейство преднорм, которые одновременно могут обращаться в нуль только в нуле пространства X. Основная конструкция индуцирования применима, и в результате её пространство X наделяется локально-выпуклой топологией полинормированного пространства с (непрерывными) преднормами pα.Полинормированные пространства — объект изучения функционального анализа.
Пример. Пусть X — топологическое векторное пространство над полем
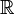 , X * — пространство непрерывных линейных функционалов на X. Каждый элемент
, X * — пространство непрерывных линейных функционалов на X. Каждый элемент  пространства X * — это непрерывная линейная функция
пространства X * — это непрерывная линейная функция 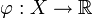 . Топология, индуцированная всеми такими функциями, называется слабой топологией пространства X. Слабой окрестностью точки x0 будет множество вида
. Топология, индуцированная всеми такими функциями, называется слабой топологией пространства X. Слабой окрестностью точки x0 будет множество видадля некоторого конечного числа функционалов
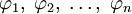 и чисел
и чисел 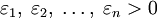 .
.Зеркальным образом вводится и *-слабая (читается: «слабая со звездой») топология на пространстве X * , так как каждый элемент x пространства X тоже задаёт линейную функцию на пространстве X * по формуле
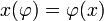 .
.Определение
Пусть дано топологическое пространство
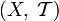 , где X — произвольное множество, а
, где X — произвольное множество, а 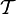 — определённая на X топология. Пусть также
— определённая на X топология. Пусть также 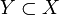 . Определим
. Определим 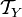 — семейство подмножеств Y следующим образом:
— семейство подмножеств Y следующим образом:Несложно проверить, что
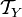 является топологией на Y. Эта топология называется индуцированной топологией
является топологией на Y. Эта топология называется индуцированной топологией 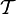 . Топологическое пространство
. Топологическое пространство 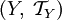 называется подпростра́нством
называется подпростра́нством 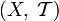 .
.Пример
Пусть дана вещественная прямая
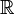 со стандартной топологией. Тогда топология, индуцированная последней на множестве всех натуральных чисел
со стандартной топологией. Тогда топология, индуцированная последней на множестве всех натуральных чисел 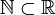 , является дискретной.
, является дискретной.
Wikimedia Foundation. 2010.