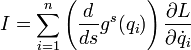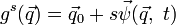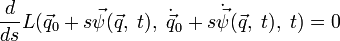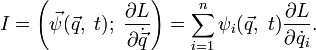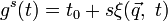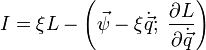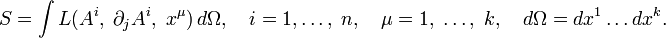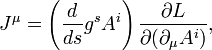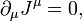Нётер теорема

Теоре́ма Эмми Нётер утверждает, что каждой симметрии физической системы соответствует некоторый закон сохранения. Так, закон сохранения энергии соответствует однородности времени, закон сохранения импульса — однородности пространства, закон сохранения момента импульса — изотропии пространства, закон сохранения электрического заряда — калибровочной симметрии и т. д.

Теорема обычно формулируется для систем, обладающих функционалом действия, и выражает собой инвариантность лагранжиана по отношению к некоторой непрерывной группе преобразований.

Теорема установлена в работах учёных гёттингенской школы Д. Гильберта, Ф. Клейна и Э. Нётер. В наиболее распространенной формулировке была доказана Эмми Нётер в 1918 году.

Формулировка

Классическая механика

Каждой однопараметрической группе диффеоморфизмов g^s(q_i), сохраняющих функцию Лагранжа, соответствует первый интеграл системы, равный

$I=\sum^n_{i=1}\left( \frac{d}{ds} g^s(q_i) \right) \frac{\partial L}{\partial \dot q_i}$

В терминах инфинитезимальных преобразований, пусть инфинитезимальное преобразование координат имеет вид

$g^s(\vec q) = \vec q_0 + s \vec \psi (\vec q,\; t)$

и функция Лагранжа 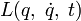$L(q,\; \dot q,\; t)$ инвариантна относительно этих преобразований, то есть

$\frac{d}{ds}L(\vec q_0 + s \vec \psi (\vec q,\; t),\; \dot \vec q_0 + s \dot \vec \psi (\vec q,\; t),\; t) = 0$

Тогда у системы существует первый интеграл, равный

$I = \left( \vec \psi (\vec q,\; t);\; \frac{\partial L}{\partial \dot \vec q} \right) = \sum^n_{i=1}\psi_i (\vec q,\; t) \frac{\partial L}{\partial \dot q_i}.$

Теорему можно обобщить на случай преобразований, затрагивающих также и время, если представить её движение как зависящее от некоторого параметра τ, причем в процессе движения t = τ. Тогда из преобразований

$g^s(\vec q) = \vec q_0 + s \vec \psi (\vec q,\; t)$

$g^s(t) = t_0 + s \xi (\vec q,\; t)$

следует первый интеграл

$I = \xi L - \left( \vec \psi - \xi \dot \vec q;\; \frac{\partial L}{\partial \dot \vec q} \right)$

Теория поля

Теорема Нётер допускает прямое обобщение на случаи систем с бесконечным числом степеней свободы, примером которых являются гравитационное и электромагнитное поле. А именно, пусть функция Лагранжа системы зависит от n потенциалов, зависящих, в свою очередь, от k координат. Функционал действия будет иметь вид

$S = \int L(A^i,\; \partial_j A^i,\; x^\mu)\, d \Omega,\quad i=1, \ldots,\; n,\quad \mu=1,\; \ldots,\; k,\quad d\Omega = dx^1\ldots dx^k.$

Пусть однопараметрическая группа g^s диффеоморфизмов пространства потенциалов сохраняет функцию Лагранжа, тогда сохраняется вектор

$J^\mu = \left( \frac{d}{ds} g^s A^i \right) \frac{\partial L}{\partial (\partial_\mu A^i)},$

называемый вектором потока Нётер. По повторяющимся индексам подразумевается суммирование, 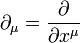$\partial_\mu = \frac{\partial}{\partial x^\mu}$. Смысл сохранения вектора потока Нётер в том, что

$\ \partial_\mu J^\mu = 0,$

поэтому поток J через любую замкнутую поверхность в пространстве координат равен 0. В частности, если выделить среди координат одну, называемую временем, и рассмотреть гиперплоскости постоянного времени, то поток J через такую гиперплоскость постоянен во времени, при условии достаточно быстрого спадения поля на бесконечности и некомпактности гиперповерхности, чтобы поток вектора через боковую границу области пространства между двумя гиперповерхностями был равен 0. В классической теории поля таким свойством обладает, например, тензор энергии-импульса для электромагнитного поля. В вакууме лагранжиан поля не зависит явно от координат, поэтому имеется сохраняющаяся величина, ассоциируемая с потоком энергии-импульса.

Законы сохранения

В классической механике законы сохранения энергии, импульса и момента импульса выводятся из однородности/изотропности лагранжиана системы — лагранжиан (функция Лагранжа) не меняется со временем сам по себе и не изменяется переносом или поворотом системы в пространстве. По сути это означает то, что при рассмотрении некой замкнутой в лаборатории системы будут получены одни и те же результаты — вне зависимости от расположения лаборатории и времени проведения эксперимента. Другие симметрии лагранжиана системы, если они есть, соответствуют другим сохраняющимся в данной системе величинам (интегралам движения); например, симметрия лагранжиана гравитационной и кулоновской задачи двух тел приводит к сохранению не только энергии, импульса и момента импульса, но и вектора Лапласа — Рунге — Ленца.

Приложения

Теорема Нётер позволяет получать значительную информацию о свойствах решений системы дифференциальных уравнений, основываясь лишь на их симметрии. Она также является одним из методов интегрирования обыкновенных дифференциальных уравнений, так как позволяет в некоторых случаях находить первые интегралы системы уравнений и таким образом понижать число неизвестных функций. Например:

• Сохранение импульса системы следует из её инвариантности относительно пространственных сдвигов. Конкретнее, если сдвиг вдоль оси X не меняет систему уравнений, то сохраняется импульс p_x вдоль этой оси.
• Сохранение момента импульса следует из инвариантности системы относительно вращений пространства.
• Закон сохранения энергии — это следствие однородности времени, позволяющей произвольным образом сдвигать начало его отсчёта.

В случае уравнений в частных производных необходимо, вообще говоря, искать бесконечное число первых интегралов. Даже зная их, обычно нелегко выписать общее решение.

В силу своей фундаментальности, теорема Нётер используется в таких областях физики, как квантовая механика, для самого введения понятий импульса, момента импульса и т. д. Инвариантность уравнений относительно некоторых симметрий становится единственной сутью этих величин и гарантирует их сохранение.

В квантовой теории поля аналогом теоремы Нётер являются тождества Уорда — Такахаши (англ.), позволяющие получить дополнительные законы сохранения. Например, сохранения электрического заряда следует из инвариантности физической системы относительно изменения фазы комплексной волновой функции частицы и соответствующей калибровки векторного и скалярного потенциала электромагнитного поля.

Заряд Нётер также используется для вычисления энтропии стационарной чёрной дыры^[1].

Примечания

1. ↑ Calculating the entropy of stationary black holes. (англ.)

Внешние ссылки

• Перевод статьи Нётер на английский
• Статья о Теореме Нётер, by John Baez (англ.)
• E. Noether’s Discovery of the Deep Connection Between Symmetries and Conservation Laws by Nina Byers
• Теорема Нётер на MathPages. (англ.)
• Symmetric energy-momentum tensor in Maxwell, Yang-Mills, and Proca theories obtained using only Noether’s theorem. (англ.)
• Giachetta G., Mangiarotti L., Sardanashvily G. On the notion of gauge symmetries of generic Lagrangian field theory. — J. Math. Phys. 50 (2009) 012903; arXiv 0807.3003.

Литература

• Арнольд В. И. Математические методы классической механики, изд. 5-ое, — М.: Едиториал УРСС, 2003, ISBN 5-354-00341-5
• Ибрагимов Н. Х. Группы преобразований в математической физике. — М.: Наука, 280 с., 1983 г.