Многообразие (топология)

Многообра́зие — пространство, которое локально выглядит как «обычное» Евклидово пространство $\R^n$. Евклидово пространство является самым простым примером многообразия. Более сложным примером может служить поверхность Земли, на которой небольшие области могут быть изображены на плоской карте, но тем не менее невозможно составить единую карту всей её поверхности.

Исследования многообразий были начаты во второй половине XIX века, они естественно возникли при изучении дифференциальной геометрии и теории групп Ли. Тем не менее, первые точные определения были сделаны только в 30-х годах XX века.

Обычно рассматриваются так называемые гладкие многообразия, то есть те, на которых есть выделенный класс «гладких» функций — в таких многообразиях можно говорить о касательных векторах и касательных пространствах. Для того, чтобы измерять длины кривых и углы, нужна ещё дополнительная структура — риманова метрика.

В классической механике гладкие многообразия служат как фазовые пространства. В общей теории относительности четырёхмерные псевдоримановы многообразия используются как модель для пространства-времени.

Топологические многообразия

n-мерное топологическое многообразие (без границы) — это хаусдорфово топологическое пространство, в котором каждая точка имеет открытую окрестность, гомеоморфную открытому подмножеству $\R^n$, то есть n-мерного Евклидова пространства.

n-мерное топологическое многообразие с краем — это хаусдорфово топологическое пространство, в котором каждая точка имеет окрестность, гомеоморфную открытому подмножеству замкнутого полупространства в $\R^n$ (считаем открытыми также объединения открытых подмножеств с пересечением их границы и граничной гиперплоскости). Точки, которые имеют открытую окрестность, гомеоморфную открытому подмножеству $\R^n$, называются внутренними, а множество всех таких точек — внутренность многообразия (это всегда непустое множество). Дополнение к внутренности называется краем, это — (n − 1)-мерное многообразие.

Обычно в определениях дополнительно предполагается, что многообразие либо паракомпактно (это эквивалентно метризуемости), либо, что ещё сильнее, имеет счётную базу (это эквивалентно тому, что многообразие вкладывается в Евклидово пространство конечной размерности).

Далее мы везде предполагаем, что многообразие имеет счётную базу.

Компактное связное многообразие без границы называется замкнутым, некомпактное связное многообразие называется открытым.

Комментарии

• Следует отметить, что введённое здесь понятие края вовсе не равносильно понятию относительной границы в общей топологии.
• Требование хаусдорфовости может показаться излишним; пример пространства, которое локально гомеоморфно евклидовому, но при этом не хаусдорфово, можно построить склеиванием двух копий вещественной прямой по всем точкам, кроме одной.

Гладкие многообразия

Гладкая структура, определённая ниже, обычно возникает в почти всех приложениях и при этом делает многообразие гораздо удобней в работе.

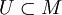Начинаем с топологического многообразия M без границы. Назовём картой гомеоморфизм $\varphi$ из открытого множества $U\subset M$ на открытое подмножество $\R^n$.

Набор карт, покрывающих всё M, называется атласом.

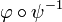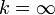Если две карты $\varphi$ и ψ накрывают одну точку в M, то их композиция $\varphi\circ\psi^{-1}$ задаёт отображение «склейки» из открытого множества $\R^n$ в открытое множество $\R^n$. Если все отображения склейки из класса C^k (то есть k раз непрерывно дифференцируемых функций), то атлас называется C^k атласом (можно также рассматривать $k=\infty$ или ω, что соответствует бесконечно дифференцируемым и аналитическим склейкам).

Пример: сфера может быть покрыта 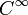$C^\infty$-атласом из двух карт на дополнениях северного и южного полюсов со стереографическими проекциями по отношению к этим полюсам.

Два C^k атласа задают одну C^k-гладкую структуру, если их объединение является C^k-атласом.

Для таких многообразий можно ввести понятия касательного вектора, касательного и кокасательного пространств и расслоений.

Для заданной C¹-гладкой структуры можно найти 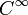$C^\infty$-гладкую структуру, задаваемую новым 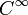$C^\infty$-атласом, который задаёт ту же C¹-гладкую структуру. Более того все такие полученные таким образом многообразия являются 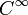$C^\infty$-диффеоморфными. Поэтому часто под гладкой структурой понимают C¹-гладкую структуру.

Не каждое топологическое многообразие допускает гладкую структуру. Примеры таких «шершавых» многообразий появляются уже в размерности четыре. Также существуют примеры топологических многообразий, которые допускают несколько различных гладких структур. Первый такой пример нестандартной гладкой структуры, так называемая сфера Милнора, был построен Милнором на семимерной сфере.

Классификация многообразий

Каждое связное одномерное многообразие без границы гомеоморфно вещественной прямой или окружности

Гомеоморфный класс замкнутой связной поверхности задаётся её Эйлеровой характеристикой и ориентируемостью. (Если ориентируемо, то это сфера с ручками, если нет, то связная сумма нескольких копий проективной плоскости)

Классификация замкнутых трёхмерных многообразий следует из гипотезы Тёрстона, которая была недавно доказана Григорием Перельманом.

Если размерность больше трёх, то классификация невозможна; более того, невозможно построить алгоритм, который определяет, является ли многообразие односвязным. Тем не менее существует классификация всех односвязанных многообразий во всех размерностях ≥ 5.

Можно также классифицировать гладкие многообразия.

• В размерностях 2 и 3 любая пара гомеоморфных многообразий является также диффеоморфной.
• В размерности 4 существуют примеры замкнутых многообразий, которые допускают бесконечное число неэквивалентных гладких структур, а открытые многообразия, как, например, 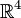$\R^4$ допускают континуум различных гладких структур.
• В размерностях 5 и выше любое топологическое многообразие допускает не более чем конечное число неэквивалентных гладких структур.

Дополнительные структуры

Часто гладкие многообразия оснащают дополнительными структурами. Вот список наиболее часто встречаемых дополнительных структур:

• Метрический тензор
• Симплектическая форма
• Комплексная структура

Обобщения

• Орбиобразие (англ.).

См. также

• Алгебраическое многообразие
• Аналитическое многообразие
• Граф-многообразие

Литература

• Дубровин Б. А., Новиков С. П., Фоменко А.Т Современная геометрия. Методы и приложения.