- КВАЗИКЛАССИЧЕСКОЕ ПРИБЛИЖЕНИЕ
- КВАЗИКЛАССИЧЕСКОЕ ПРИБЛИЖЕНИЕ
-
квантовой механики (Венцеля — Крамерса — Бриллюэна метод), приближённый метод решения задач квант. механики, применимый, когда и квант. и классич. описание движения ч-цы дают близкие результаты; впервые использован нем. физиком Г. Венцелем, англ. физиком Г. Крамерсом и франц. физиком Л. Бриллюэном в 1926. С точки зрения общей теории волн. полей К. п. соответствует такому описанию, при к-ром основным явл. рассмотрение лучей («геом. приближение»), а «волновые» эффекты выступают как малые поправки. Такое описание приемлемо, если длина волны (в квант. механике — длина волны де Бройля) достаточно мала — много меньше всех масштабов неоднородностей действующих на ч-цу внеш. полей. Кроме того, необходимо, чтобы длина волны медленно менялась от точки к точке. Т. к. длина волны де Бройля l равна отношению постоянной Планка h к импульсу р, к-рый связан с полной ? и потенциальной U(х) энергиями соотношением?=р2/2m+U(х)(где х — координата),К. п. применимо лишь в случаях, когда U(х) меняется достаточно медленно с изменением х.Формально К. п. сводится к вычислению действия S в виде разложения в ряд: S=S0+S1+S2+.., первый член к-рого не зависит от h (классич. действие S0), второй пропорц. h, третий пропорц. h2 и т. д. Найдя S, можно получить и волн. ф-цию y, равную: y=ехр(2piS/h). Обычно ограничиваются членом S1. Получаемая при этом y наз. квазиклассич. волн. ф-цией, yкп.Важный частный случай — движение ч-цы в конечной области пр-ва. При таком финитном движении внутри нек-рой потенциальной ямы К. п. не может быть применимым везде; это ясно хотя бы из того, что, доходя до «стенки» ямы, ч-ца (на языке классич. физики) на мгновение останавливается, т. е. р обращается в нуль, а следовательно, l®?. Для окрестностей вблизи таких точек поворота нужно искать y на основе точного квантовомеханич. Шредингера уравнения, а затем потребовать, чтобы между yкп и y был непрерывный переход при приближении к точкам поворота. Оказывается, что из требований этой непрерывности и однозначности y без дополнит. предположений вытекают условия квантования Бора.Применимость К. п. оправдана лишь при больших значениях квантовых чисел.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- КВАЗИКЛАССИЧЕСКОЕ ПРИБЛИЖЕНИЕ
-
квантовой механики (Венцеля - Крамерса - Бриллюэна метод, ВКБ метод) - приближённый метод нахождения волновой ф-ции и уровней энергии квантовой системы при условии, что длина волны де Бройля lчастиц системы много меньше характерных размеров R изменения потенциала. В условиях К. п. квантовое неопределённостей соотношение позволяет построить волновой пакет, в к-ром неопределённости координаты и импульса гораздо меньше самих этих величин. Такой пакет будет двигаться, подчиняясь законам классич. механики с точностью до малых величин порядка l/R.В простейшем случае точечной частицы массы m с заданной энергией E, движущейся по законам классич. механики во внеш. поле с потенциалом U(r), модуль импульса р(r)в данной точке пространства rравен p(r)-[2m(S-U(r))]l/2.Длина волны связана с импульсом соотношением де Бройля l(r)=h/p(r).Критерий применимости К. п. таков:
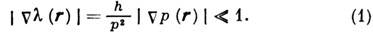
Движение квантовой частицы в тех же условиях определяется Шрёдингера уравнением: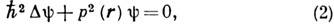
где y - волновая ф-ция частицы. В одномерном случае (потенциал и волновая ф-ция зависят лишь от одной координаты х )приближённые решения ур-ния (2) в классически доступной области E>U(x )имеют вид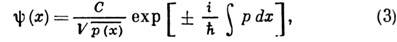
где С - постоянная. Решения (3) представляют собой простейшее обобщение плоской волны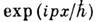 наслучай медленно меняющегося р( х).Предэкспоненц. множитель обеспечивает закон сохранения числа частиц, т. е. независимость потока числа частиц
наслучай медленно меняющегося р( х).Предэкспоненц. множитель обеспечивает закон сохранения числа частиц, т. е. независимость потока числа частиц 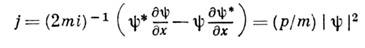
от координаты (звёздочка означает комплексное сопряжение).Решения (3) с той же точностью справедливы и в классически недоступной области E<U(x),Однако в этом случае величина р( х )становится чисто мнимой. Поэтому одно из решений экспоненциально убывает, а другое растёт по мере удаления в классически недоступную область. Эти решения описывают чисто квантовый эффект подбарьерного проникновения частиц. Критерий (1) не выполняется вблизи классич. точек поворота х 0,где U( х0)=E.Если U( х )регулярен в точке х0, то вблизи неё ур-ние Шрёдингера можно приближённо заменить ур-нием с линейным потенциалом U(x)=U'( х0)( х-х0), к-рое сводится к ур-нию Эйри (см. Эйри функция).Его решения: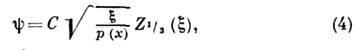
где Z1/3(x) - любое решение ур-ния Бесселя с индексом 1/3 (см. Цилиндрические функции )и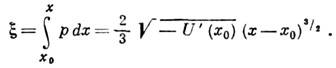
Замена точного ур-ния Шрёдингера приближённым вблизи нулей и особенностей ф-ции р2( х )носит назв. метода эталонных ур-ний. Так, вблизи простого нуля ф-ции р2( х )эталонным является ур-ние Эйри; если близкими оказываются два простых нуля, то эталонным является ур-ние параболич. цилиндра (см. Параболического цилиндра функции);при сближении простого нуля и полюса эталонным оказывается вырожденное гипергеом. ур-ние (см. Вырожденная гипергеометрическая функция). Во всех этих случаях известны аналитич. свойства решений эталонных ур-ний. Возможны и более сложные эталонные ур-ния, решения к-рых пока не исследованы. <Решения эталонного ур-ния (4) плавно сшиваются с квазиклассич. решениями (3), определяя тем самым правила перехода через точки поворота. В частности, то из решений (3), к-рое экспоненциально убывает в классически недоступной области, в разрешённой области ведёт себя как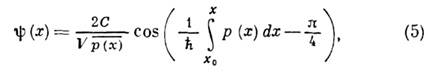
где х0- классич. точка поворота. Если классически доступная область ограничена обычными точками поворота x1 х2,то уровни энергии определяются правилами квантования Бора - Зоммерфельда: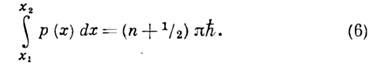
Здесь n - квантовое число, нумерующее уровни. При переходе к классич. механике величина nиграет роль адиабатического инварианта. Если одна или обе границы классич. движения близки к особенностям потенциала, то в правой части ур-ния (6) вместо слагаемого 1/2 появляется не зависящая от п постоянная g, значение к-рой определяется характером особенности. <В 1913 Н. Бор (N. Bohr) постулировал правила квантования (6) и с их помощью впервые интерпретировал эксперим. спектры поглощения атомов водорода. В силу спец. симметрии квазиклассич. уровни энергии атома водорода совпадают с точными. <Пусть потенциал U( х )таков, что в нём имеется две области классически разрешённого движения, одна из к-рых ограничена (рис.).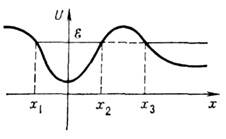
Классич. частица, находящаяся в потенц. яме, не сможет покинуть её. Но квантовая частица имеет отличную от нуля волновую ф-цию и в подбарьерной области. Выход частицы из потенц. ямы сквозь барьер является квантовым эффектом, наз. туннелированием (туннельным проникновением; см. Туннельный эффект).Вероятность туннелирования за единицу времени определяется ур-нием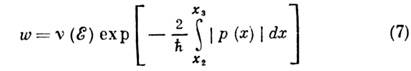
где v(E)- классич. частота движения частиц в потенц. яме. Множитель v(E) возникает из условия нормировки волновой ф-ции в классически доступной области. Представление о квантовом туннелировании и его количеств, выражение (7) были впервые применены Г. А. Гамовым (G. Gamov) для объяснения альфа-распада. Другим сугубо квантовым эффектом является oтpaжение потенц. барьером частицы с энергией, большей высоты барьера. Если потенциал является аналитич. ф-цией х, то в К. п. коэф. надбарьерного отражения (доля отраженных частиц) равен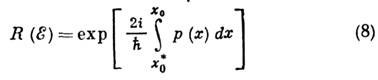
Интегрирование в показателе экспоненты происходит вдоль контура в комплексной плоскости х, идущего из ближайшей к веществ, оси комплексной точки поворота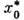 в ниж. полуплоскости к комплексно сопряжённой точке поворота х0.Ф-лы (7) и (8) применимы в том случае, когда показатели экспонент велики. <Надбарьерное отражение является частным случаем процесса, запрещённого классич. механикой. В квантовой механике такие процессы, вообще говоря, возможны, но имеют экспоненциально малую вероятность. Классич. траектория такого процесса, т. е. решение вариационного ур-ния dS=0, существует, но оказывается комплексной. Комплексно и действие S вдоль траектории. Вероятность классически запрещённого перехода определяется ф-лой
в ниж. полуплоскости к комплексно сопряжённой точке поворота х0.Ф-лы (7) и (8) применимы в том случае, когда показатели экспонент велики. <Надбарьерное отражение является частным случаем процесса, запрещённого классич. механикой. В квантовой механике такие процессы, вообще говоря, возможны, но имеют экспоненциально малую вероятность. Классич. траектория такого процесса, т. е. решение вариационного ур-ния dS=0, существует, но оказывается комплексной. Комплексно и действие S вдоль траектории. Вероятность классически запрещённого перехода определяется ф-лой 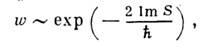
где действие взято вдоль классич. пути с мин. мнимой частью ImS. Вычисление предэкспоненц. множителя требует конкретизации задачи. <Задача о переходах в квантовой системе часто решается методом адиабатического приближения, сходным с квазиклассическим. Необходимым условием применимости адиабатич. приближения является возможность разделения движений на быстрые и медленные. Так, в случае атомных соударений движение ионов можно считать медленным, а движение электронов быстрым. Если система помещена в переменное внеш. поле, его частоты должны быть малы по сравнению с характерными частотами системы. В адиабатич. приближении уровни энергии Ei квантовой системы можно считать параметрически зависящими от времени t.Условие адиабатичности нарушается при пересечении любых двух уровней E1 и E2 (см. Пересечение уровней).В небольшом интервале времени около момента пересечения двух термов происходят переходы между ними. Вблизи точки пересечения справедлива эталонная система двух ур-ний для амплитуд состояний, являющаясяаналогом ур-ния Эйри. Вероятность перехода определяется ф-лой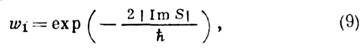
где действие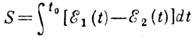 , a t0 - момент пересечения термов, <находящийся, вообще говоря, в комплексной плоскости. При двукратном прохождении точки пересечения вероятность перехода равна w2=2w1(1- w1). Возмущение V, приводящее к переходу между термами невозмущённой системы, приводит к отталкиванию уровнен и невозможности их пересечения при веществ, временах. Если возмущение V мало по сравнению с характерной разностью энергий вдали от точки пересечения, то момент t0 недалёк от веществ. оси. В этом случае
, a t0 - момент пересечения термов, <находящийся, вообще говоря, в комплексной плоскости. При двукратном прохождении точки пересечения вероятность перехода равна w2=2w1(1- w1). Возмущение V, приводящее к переходу между термами невозмущённой системы, приводит к отталкиванию уровнен и невозможности их пересечения при веществ, временах. Если возмущение V мало по сравнению с характерной разностью энергий вдали от точки пересечения, то момент t0 недалёк от веществ. оси. В этом случае 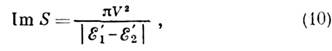
где E'1,E'2 - производные от невозмущённых уровней энергии в точке пересечения. В случае, когда медленным является относит, движение двух ионов в молекуле, E'i=vFi, где v - скорость движения ядер вблизи точки пересечения термов, Fi - сила, действующая на ядра, когда электроны находятся в состоянии с номером i. Подставляя (9) и (10) в выражение для w2, получаем ф-лу Ландау - Зинера: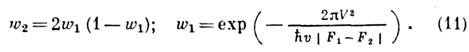
Если один из уровней принадлежит непрерывному спектру, то ф-ла (11) описывает явление предиссоциации молекулы. <К. п. с известными оговорками обобщается на случай движения в многомерном пространстве. Волновую ф-цию в этом случае можно записать в виде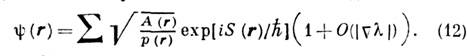
Здесь S(r) - классич. действие, подчиняющееся Гамильтона - Якоби уравнению:(СS)2 = p2(r);величина А-1(r) - относит, площадь сечения бесконечно тонкого пучка классич. траекторий, проведённого нормально к импульсу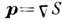 ; суммирование в (12) проводится по всем классич. траекториям, проходящим через заданную точку r.Решение (12) обеспечивает закон сохранения числа частиц. Ф-ция А(r)удовлетворяет ур-нию
; суммирование в (12) проводится по всем классич. траекториям, проходящим через заданную точку r.Решение (12) обеспечивает закон сохранения числа частиц. Ф-ция А(r)удовлетворяет ур-нию 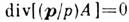 , эквивалентному ур-нию непрерывности для пучка частиц. Аналогичное построение в оптике наз. методом эйконала или геометрической оптики методом. Площадь сечения пучка траекторий пропорц. произведению гл. радиусов кривизны поверхности волнового фронта S=const. Поверхности, на к-рых А-1(r)обращается в нуль, наз. каустиками. Они являются огибающими классич. траекторий, отделяющими классически доступные области от недоступных, подобно точкам поворота в одномерной задаче. В классически недоступной области волновая ф-ция по-прежнему имеет вид (12), но S(r)становится чисто мнимым, так что волновая функция экспоненциально убывает. <Вблизи каустик, но вдали от их особых точек волновая ф-ция сравнительно быстро меняется по нормали и медленно в касательной к каустике плоскости. Приближённое решение вблизи каустик, как и в одномерном случае, подчиняется эталонным уравнениям, простейшим и наиболее типичным из к-рых является уравнение Эйри. Решение эталонных уравнений позволяет "сшить" квазиклассич. волновые ф-ции по обе стороны каустики. <Построение квазиклассич. волновых ф-ций, данное выше, обобщается на случай системы мн. частиц, а такжена случай произвольной зависимости энергии от импульса, что важно в теории твёрдого тела. <К. п. в многомерном случае, данное ур-нием (12), осмысленно только при конечном и не слишком большом числе траекторий, проходящих через данную точку. Для этого необходимо, чтобы классич. движение было устойчивым хотя бы в нек-рых областях. Др. словами, нек-рая часть фазового пространства должна расслаиваться на инвариантные торы (см. Гамильтонова система), по к-рым движется классич. система. Тогда правила квантования Бора - Зоммерфельда принимают вид
, эквивалентному ур-нию непрерывности для пучка частиц. Аналогичное построение в оптике наз. методом эйконала или геометрической оптики методом. Площадь сечения пучка траекторий пропорц. произведению гл. радиусов кривизны поверхности волнового фронта S=const. Поверхности, на к-рых А-1(r)обращается в нуль, наз. каустиками. Они являются огибающими классич. траекторий, отделяющими классически доступные области от недоступных, подобно точкам поворота в одномерной задаче. В классически недоступной области волновая ф-ция по-прежнему имеет вид (12), но S(r)становится чисто мнимым, так что волновая функция экспоненциально убывает. <Вблизи каустик, но вдали от их особых точек волновая ф-ция сравнительно быстро меняется по нормали и медленно в касательной к каустике плоскости. Приближённое решение вблизи каустик, как и в одномерном случае, подчиняется эталонным уравнениям, простейшим и наиболее типичным из к-рых является уравнение Эйри. Решение эталонных уравнений позволяет "сшить" квазиклассич. волновые ф-ции по обе стороны каустики. <Построение квазиклассич. волновых ф-ций, данное выше, обобщается на случай системы мн. частиц, а такжена случай произвольной зависимости энергии от импульса, что важно в теории твёрдого тела. <К. п. в многомерном случае, данное ур-нием (12), осмысленно только при конечном и не слишком большом числе траекторий, проходящих через данную точку. Для этого необходимо, чтобы классич. движение было устойчивым хотя бы в нек-рых областях. Др. словами, нек-рая часть фазового пространства должна расслаиваться на инвариантные торы (см. Гамильтонова система), по к-рым движется классич. система. Тогда правила квантования Бора - Зоммерфельда принимают вид 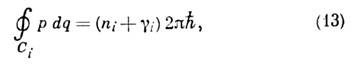
где р - обобщённый импульс, q - обобщённая координата, интегрирование в (13) ведётся по одной из независимых замкнутых кривых на торе, вообще говоря, не совпадающей с классич. траекторией, gi - число, зависящее от того, сколько раз кривая Сi касается каустики. Если известна, хотя бы приближённо, к.-н. замкнутая устойчивая классич. траектория, то в её окрестности правила квантования (13) позволяют найти большое число уровней. Соответствующие волновые ф-ции локализованы в узком канале вокруг классич. траектории, площадь канала s@ЦRl,где R - характерный линейный размер траектории. <Наиб. просто квазиклассич. правила квантования применяются для высоковозбуждённых состояний систем с почти разделяющимися переменными. Если невозмущённая система невырождена, т. е. частоты wi=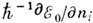 несоизмеримы (S0(n) - энергия невозмущённой системы, ni - квантовые числа), то энергия изменяется на величину <V> возмущения V, усреднённого по всем фазовым переменным, а волновая ф-ция сосредоточена в окрестности
несоизмеримы (S0(n) - энергия невозмущённой системы, ni - квантовые числа), то энергия изменяется на величину <V> возмущения V, усреднённого по всем фазовым переменным, а волновая ф-ция сосредоточена в окрестности 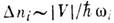 около фиксированных значений n0i.Если нек-рые из частот соизмеримы, напр., две частоты w1 и w2 равны друг другу, то разность соответствующих угл. переменных j1-j2 медленно меняется, а квантовое число k=n1-n2 изменяется в широком интервале. Усреднённое по быстрым фазам возмущение V является гамильтонианом для медленных переменных. <Правила перехода от квантовых к классич. величинам таковы. Классич. частоты определяют расстояния между соседними уровнями. Матричные элементы физ. величин переходят в фурье-компоненты соответствующих классич. величин. Наконец, перестановочным соотношениям операторов в квантовой механике соответствуют классические Пуассона скобки, помноженные на
около фиксированных значений n0i.Если нек-рые из частот соизмеримы, напр., две частоты w1 и w2 равны друг другу, то разность соответствующих угл. переменных j1-j2 медленно меняется, а квантовое число k=n1-n2 изменяется в широком интервале. Усреднённое по быстрым фазам возмущение V является гамильтонианом для медленных переменных. <Правила перехода от квантовых к классич. величинам таковы. Классич. частоты определяют расстояния между соседними уровнями. Матричные элементы физ. величин переходят в фурье-компоненты соответствующих классич. величин. Наконец, перестановочным соотношениям операторов в квантовой механике соответствуют классические Пуассона скобки, помноженные на 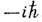 Общепринято представление о том, что в случае, когда классич. движение хаотично, квантовая система демонстрирует нерегулярное поведение высоковозбуждённых уровней. Их ср. плотность r(E) определяется, как и в случае свободных частиц, производной по энергии от объёма классически доступной области в фазовом пространстве. Напр., для частицы, движущейся в потенц. поле U(r)в трёхмерном пространстве
Общепринято представление о том, что в случае, когда классич. движение хаотично, квантовая система демонстрирует нерегулярное поведение высоковозбуждённых уровней. Их ср. плотность r(E) определяется, как и в случае свободных частиц, производной по энергии от объёма классически доступной области в фазовом пространстве. Напр., для частицы, движущейся в потенц. поле U(r)в трёхмерном пространстве 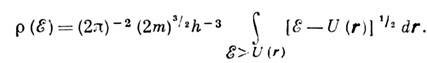
Но расстояния между уровнями флуктуируют. Задача о распределении расстояний между уровнями не решена, намечены только нек-рые подходы к ней. Мало известно о статистич. характеристиках волновых ф-ций. Численные методы и теоретич. соображения показывают, что квадрат модуля волновой ф-ции максимален вблизи периодич. классич. траекторий, даже если они неустойчивы. Энергия системы на такой траектории соответствует максимуму плотности состояний. <Для вычисления вероятности туннелирования в многомерном случае необходимо найти траекторию, проходящуюв классически недоступной области, вдоль к-рой минимален модуль мнимого действия. Вероятность туннелирования в основном определяется экспоненциально малым фактором ехр(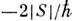 ), где S - мнимое действие вдоль туннельной траектории. Предэкспоненц. множитель находится с помощью правил сшивки на каустике по известной волновой ф-ции внутри потенц. ямы. <К. п. легко обобщается на нестационарный случай, если в ф-ле (12) подразумевать под S зависящее от времени действие, подчиняющееся нестационарному ур-нию Гамильтона - Якоби. <К. п. можно получить из представления Фейнмана волновой ф-ции в виде интеграла по всем путям (см. Функционального интеграла метод),если считать
), где S - мнимое действие вдоль туннельной траектории. Предэкспоненц. множитель находится с помощью правил сшивки на каустике по известной волновой ф-ции внутри потенц. ямы. <К. п. легко обобщается на нестационарный случай, если в ф-ле (12) подразумевать под S зависящее от времени действие, подчиняющееся нестационарному ур-нию Гамильтона - Якоби. <К. п. можно получить из представления Фейнмана волновой ф-ции в виде интеграла по всем путям (см. Функционального интеграла метод),если считать 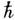 малой величиной. Тогда осн. вклад в интеграл вносит малая окрестность путей, вдоль к-рых действие минимально, т. е. классич. траекторий. К. п. можно использовать в чисто матем. целях для вычисления асимптотич. вида решений обыкновенных линейных дифференц. ур-ний второго порядка: y "+q2(x)y=0 [ср. с ур-нием (2)]. К такому виду приводятся ур-ния для гипергеометрических функций и нек-рых важных частных случаев этих ф-ций (ф-ций Бесселя, Лежандра, Лагерра и др.). Асимптотич. решения этих ур-ний имеют общий вид
малой величиной. Тогда осн. вклад в интеграл вносит малая окрестность путей, вдоль к-рых действие минимально, т. е. классич. траекторий. К. п. можно использовать в чисто матем. целях для вычисления асимптотич. вида решений обыкновенных линейных дифференц. ур-ний второго порядка: y "+q2(x)y=0 [ср. с ур-нием (2)]. К такому виду приводятся ур-ния для гипергеометрических функций и нек-рых важных частных случаев этих ф-ций (ф-ций Бесселя, Лежандра, Лагерра и др.). Асимптотич. решения этих ур-ний имеют общий вид 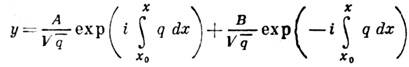
и подчиняются эталонным ур-ниям вблизи разл. особых точек. Если q2( х) - аналитич. ф-ция, то такие решения можно продолжить в комплексную плоскость х.Однако на нек-рых линиях в комплексной плоскости, наз. линиями Стокса, коэф. А и В могут резко меняться. В частности, из каждой точки поворота х0,вк-рой g2(x0)=0,выходят три линии Стокса под углом 120°.Решение у 0,к-рое ведёт себя как ехр (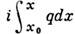 ) на биссектрисе одного из углов (убывающая экспонента), приходит с неизменным коэф. на линии Стокса, ограничивающие этот угол. Но на третьей линии Стокса появляется вторая экспонента с коэф. bi. Матрица, преобразующая коэф. А, В при переходе с одной линии Стокса на другую, наз. матрицей монодромии. Знание этой матрицы позволяет "сшивать" квазиклассич. асимптотики в разных областях без детального исследования эталонных уравнений. В частности, приведённое правило изменения коэффициентов в окрестности точки поворота эквивалентно правилу сшивки (4).
) на биссектрисе одного из углов (убывающая экспонента), приходит с неизменным коэф. на линии Стокса, ограничивающие этот угол. Но на третьей линии Стокса появляется вторая экспонента с коэф. bi. Матрица, преобразующая коэф. А, В при переходе с одной линии Стокса на другую, наз. матрицей монодромии. Знание этой матрицы позволяет "сшивать" квазиклассич. асимптотики в разных областях без детального исследования эталонных уравнений. В частности, приведённое правило изменения коэффициентов в окрестности точки поворота эквивалентно правилу сшивки (4).
Историчегкая справка. Как метод решения дифференц. ур-ний К. п. впервые применялось Ж. Лиувиллем (J. Liouville) в 1837. Дальнейшее развитие К. п. нашло в трудах Рэлея (J. Rayleigh, 1912) и X. Джефриса (Н. Jeffreys, 1923). В связи с задачами квантовой механики К. п. было вновь изобретено Г. Венцелем (G. Wentzel), X. Крамерсом (Н. A. Kramers) и Л. Бриллюэном (L. N. Brillouin) в 1926, вследствие чего оно часто и наз. методом ВКБ (WKB или JWKB). Крамере, в частности, установил правила сшивки вблизи точки поворота. <Квазиклассич. правила квантования были угаданы Н. Бором (N. Bohr) в 1913, за 13 лет до создания регулярной квантовой механики. Лит.:Ландау Л. Д., Лифшиц Е. М., Квантовая механика, 3 изд., М., 1974; Мигдал А. Б., Качественные методы в квантовой теории, М., 1975; Маслов В. П., Федорюк М. В., Квазиклассическое приближение для уравнений квантовой механики, М., 1976. В. Л. Покровский.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
