ВЕЩЕСТВЕННОЕ АНАЛИТИЧЕСКОЕ ПРОСТРАНСТВО
- ВЕЩЕСТВЕННОЕ АНАЛИТИЧЕСКОЕ ПРОСТРАНСТВО
- аналитическое пространство над полем R действительных чисел. В отличие от комплексных аналитич. ространств, структурные пучки В. а. п. могут не быть когерентными пучками. В. а. п. наз. когерентным, если его структурный пучок когерентен. Все вещественные аналитич. многообразия (т. е. гладкие В. а. п.) являются когерентными В. а. п.
Пусть  - росток в точке авещественного аналитич. одмножества пространства
- росток в точке авещественного аналитич. одмножества пространства  . Тогда определен росток в точке акомплексного аналитич. одмножества
. Тогда определен росток в точке акомплексного аналитич. одмножества  пространства
пространства  , обладающий следующими эквивалентными свойствами: а)
, обладающий следующими эквивалентными свойствами: а) 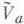 есть пересечение всех ростков комплексных аналитич. множеств, содержащих
есть пересечение всех ростков комплексных аналитич. множеств, содержащих  ; 6) если
; 6) если  - аналитич. алгебра ростка
- аналитич. алгебра ростка  , то
, то 
есть аналитич. алгебра ростка  . Росток
. Росток  наз. комплексификацией ростка
наз. комплексификацией ростка  , а
, а  - вещественной частью ростка
- вещественной частью ростка  . Аналогично для всякого когерентного В. а. п. Xможно построить комнлек-сификацию
. Аналогично для всякого когерентного В. а. п. Xможно построить комнлек-сификацию  , являющуюся комплексным аналитич. ространством. При этом Xбудет обладать в
, являющуюся комплексным аналитич. ространством. При этом Xбудет обладать в  фундаментальной системой окрестностей, являющихся Штейна пространствами.
фундаментальной системой окрестностей, являющихся Штейна пространствами.
Теория когерентных В. а. п. аналогична теории комплексных пространств Штейна. Глобальные сечения всякого когерентного аналитического пучка модулей Fна когерентном В. а. п. Xпорождают модули ростков его сечений в любой точке пространства X, и все группы  равны нулю при
равны нулю при  .
.
Для всякого конечномерного когерентного В. а. п.  существует морфизм
существует морфизм
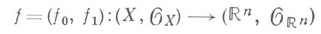
такой, что  - собственное взаимно однозначное отображение пространства Xна когерентное подпространство в
- собственное взаимно однозначное отображение пространства Xна когерентное подпространство в  , причем
, причем  - вложение в гладких точках пространства X. В частности, всякое (хаусдорфово и счетное в бесконечности) вещественное аналитич. многообразие изоморфно вещественному аналитич. одмногообразию в
- вложение в гладких точках пространства X. В частности, всякое (хаусдорфово и счетное в бесконечности) вещественное аналитич. многообразие изоморфно вещественному аналитич. одмногообразию в  . Для приведенного когерентного В. а. п. Xмножество классов изоморфных вещественно аналитич. лавных расслоений со структурной вещественной группой Ли G, допускающей комплексификацию, и базой Xнаходится во взаимно однозначном соответствии с множеством классов изоморфных топологич. главных расслоений с той же структурной группой G.
. Для приведенного когерентного В. а. п. Xмножество классов изоморфных вещественно аналитич. лавных расслоений со структурной вещественной группой Ли G, допускающей комплексификацию, и базой Xнаходится во взаимно однозначном соответствии с множеством классов изоморфных топологич. главных расслоений с той же структурной группой G.
Лит.:[1] Espaces analytiques, Buc., 1971, р. 149-57.
Д. А. Пономарев.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Полезное
Смотреть что такое "ВЕЩЕСТВЕННОЕ АНАЛИТИЧЕСКОЕ ПРОСТРАНСТВО" в других словарях:
АНАЛИТИЧЕСКОЕ ПРОСТРАНСТВО — обобщение понятия аналитического многообразия. Локальной моделью (и одновременно важнейшим примером) аналитич. ространства над полным недискретно нормированным полем kявляется аналитическое множество в области n мерного пространства над полем k,… … Математическая энциклопедия
ГЛАВНОЕ АНАЛИТИЧЕСКОЕ РАССЛОЕНИЕ — локально тривиальное аналитич. расслоение, на слоях к рого просто транзитивно и аналитически действует структурная группа Ли; то есть Г. а. р. есть четверка аналитические пространства над полем аналитич. отображение, G группа Ли над k,… … Математическая энциклопедия
Вещественное число — Вещественное, или действительное число [1] математическая абстракция, возникшая из потребности измерения геометрических и физических величин окружающего мира, а также проведения таких операций как извлечение корня, вычисление логарифмов, решение… … Википедия
АНАЛИТИЧЕСКОЕ МНОГООБРАЗИЕ — многообразие с аналитич. атласом. Структура n мерного аналитич. многообразия над полным недискретно нормированным полем kна топологич. пространстве Мопределяется заданием на Маналитич. атласа над k, т. е. набора карт со значениями в kn,… … Математическая энциклопедия
АЛГЕБРАИЧЕСКАЯ ПОВЕРХНОСТЬ — двумерное алгебраическое многообразие. Вместе с алгебраическими кривыми А. п. представляют собой наиболее изученный класс алгебраич. многообразий. Богатство задач и идей, применяемых для их решения, делает теорию А. п. одним из самых интересных… … Математическая энциклопедия
ЭРМИТОВА МЕТРИКА — 1) Э. м. в комплексном векторном пространстве V положительно определенная эрмитова форма в V. Пространство V, снабженное Э. м., наз. унитарным (или комплексно евклидовым, или эрмитовым векторным) пространством, а Э. м. в нем эрмитовым скалярным… … Математическая энциклопедия
Список статей по математической логике — Это служебный список статей, созданный для координации работ по развитию темы. Данное предупреждение не ус … Википедия
Кант — (Immanuel Kant, первонач. Cant) основатель философского критицизма, представляющего главную поворотную точку в истории человеческой мысли, так что все развитие философии, если не по содержанию, то по отношению мысли к этому содержанию, должно… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
 - росток в точке авещественного аналитич. одмножества пространства
- росток в точке авещественного аналитич. одмножества пространства  . Тогда определен росток в точке акомплексного аналитич. одмножества
. Тогда определен росток в точке акомплексного аналитич. одмножества  пространства
пространства  , обладающий следующими эквивалентными свойствами: а)
, обладающий следующими эквивалентными свойствами: а) 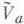 есть пересечение всех ростков комплексных аналитич. множеств, содержащих
есть пересечение всех ростков комплексных аналитич. множеств, содержащих  ; 6) если
; 6) если  - аналитич. алгебра ростка
- аналитич. алгебра ростка  , то
, то 
 . Росток
. Росток  наз. комплексификацией ростка
наз. комплексификацией ростка  , а
, а  - вещественной частью ростка
- вещественной частью ростка  . Аналогично для всякого когерентного В. а. п. Xможно построить комнлек-сификацию
. Аналогично для всякого когерентного В. а. п. Xможно построить комнлек-сификацию  , являющуюся комплексным аналитич. ространством. При этом Xбудет обладать в
, являющуюся комплексным аналитич. ространством. При этом Xбудет обладать в  фундаментальной системой окрестностей, являющихся Штейна пространствами.
фундаментальной системой окрестностей, являющихся Штейна пространствами. равны нулю при
равны нулю при  .
. существует морфизм
существует морфизм 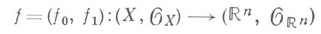
 - собственное взаимно однозначное отображение пространства Xна когерентное подпространство в
- собственное взаимно однозначное отображение пространства Xна когерентное подпространство в  , причем
, причем  - вложение в гладких точках пространства X. В частности, всякое (хаусдорфово и счетное в бесконечности) вещественное аналитич. многообразие изоморфно вещественному аналитич. одмногообразию в
- вложение в гладких точках пространства X. В частности, всякое (хаусдорфово и счетное в бесконечности) вещественное аналитич. многообразие изоморфно вещественному аналитич. одмногообразию в  . Для приведенного когерентного В. а. п. Xмножество классов изоморфных вещественно аналитич. лавных расслоений со структурной вещественной группой Ли G, допускающей комплексификацию, и базой Xнаходится во взаимно однозначном соответствии с множеством классов изоморфных топологич. главных расслоений с той же структурной группой G.
. Для приведенного когерентного В. а. п. Xмножество классов изоморфных вещественно аналитич. лавных расслоений со структурной вещественной группой Ли G, допускающей комплексификацию, и базой Xнаходится во взаимно однозначном соответствии с множеством классов изоморфных топологич. главных расслоений с той же структурной группой G.