БУЛЕВЫХ ФУНКЦИЙ НОРМАЛЬНЫЕ ФОРМЫ

формулы специального вида, реализующие булевы функции. Различают дизъюнктивные, нормальные формы (д. н. ф.; см. Булевых функций минимизация).и конъюнктивные нормальные формы (к. н. ф.). Произведение где при при , наз. элементарной конъюнкцией ранга , если все переменные в нем различны; 1 считается элементарной конъюнкцией нулевого ранга. Логическая сумма наз. элементарной дизъюнкцией ранга r, если все переменные в ней различны; 0 считается элементарной дизъюнкцией нулевого ранга.

Формула где - различные элементарные конъюнкции рангов соответственно, наз. д. н. ф., а число _ сложностью этой д. н. ф.; формула где - различные элементарные дизъюнкции рангов соответственно, наз. к. н. ф., а число - .сложностью этой к. н. ф. Всякая булева функция, отличная от тождественного нуля, может быть задана д. н. ф. и, вообще говоря, неоднозначно. Аналогичный факт имеет место для к. н. ф. п функций, не равных тождественно единице.

По таблице, задающей булеву функцию легко строится совершенная д. н. ф. где и наборы таковы, что . Совершенная д. н. ф., реализующая булеву функцию f, строится однозначно. Аналогично определяется совершенная к. н. ф. Так как "почти все" булевы функции имеют число единичных наборов в пределах от до то асимптотич. сложность совершенной д. н. ф. для "почти всех" булевых функций равна Максимальная сложность совершенной д. н. ф. для функций от n переменных достигается для функций, равных 0, в одной точке. Она равна .

Основной задачей в теории Б. ф. н. ф. является задача минимизации булевых функций, т. е. построение для произвольной булевой функции к. н. ф. или д. н. ф. минимальной сложности -м инимальной к. <н. ф. или д. н. ф. (см. Булевых функций минимизация, Алгоритм локальный). При этом, в силу принципа двойственности, достаточно рассматривать только д. н. ф. В связи с задачей минимизации булевых функций рассматриваются также д. н. ф. сокращенная, тупиковые, кратчайшие и минимальные. Важной задачей теории д. н. ф. является отыскание их числовых характеристик, а также характеристик, связывающих различные типы д. н. ф. одной функции.

Сокращенная д. н. ф. строится по булевой функции однозначно с помощью достаточно простых алгоритмов. Ее важнейшим свойством является то, что всякая минимальная д. н. ф. функции и хотя бы одна кратчайшая получаются из сокращенной д. н. ф. удалением нек-рых элементарных конъюнкций. Поэтому многие алгоритмы минимизации используют сокращенные д. н. ф. в качестве исходного задания булевой функции. В связи с этим большой интерес представляет определение сложности сокращенных д. н. ф. для "почти всех" функций и выяснение абсолютного максимума этой сложности. Если - число элементарных конъюнкций в сокращенной д. н. ф. булевой функции и

то имеют - место следующие оценки:

и для "почти всех" булевых функций

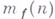Из этих результатов и оценок сложности совершенной д. н. ф. видно, что сложность сокращенной д. н. ф. существенно больше сложности совершенной д. н. ф. как в "типичном", так и в "рекордном" случаях. В отличие от совершенной и сокращенной д. н. ф., у одной булевой функции может быть много тупиковых и минимальных д. н. ф. Пусть - число тупиковых д. н. ф., - число минимальных д. н. ф. булевой функции

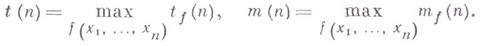
Имеют место следующие оценки:

и для "почти всех" булевых функций

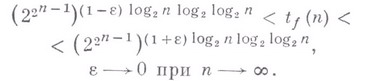
Верхняя оценка для и оценка для "почти всех" функции, отличных от тривиальных, пока (1977) не найдены. Большой интерес в задачах минимизации булевых функций представляют оценки сложности тупиковых д. н. ф. и минимальных д. н. <ф. Пусть - число элементарных конъюнкций в тупиковой д. н. ф. Тфункции - число элементарных конъюнкций в кратчайших д. <н. <ф. функции ,

Имеют место следующие оценки:

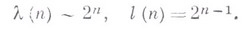
У "почти всех" булевых функций для почти всех тупиковых д. н. ф. Т:

Для "почти всех" булевых функций

Эти оценки показывают, что кратчайшие (а также минимальные) д. н. ф. составляют у "почти всех" булевых функций малую долю от числа тупиковых д. н. ф. Существуют также оценки относительной сложности тупиковых д. н. ф. и кратчайших д. н. ф. булевых функций. Пусть - максимальное число элементарных конъюнкций'в тупиковой д. н. ф. функции . Для "почти всех" булевых функций

Максимальное значение отношения оценивается снизу величиной при . Получены также оценки для величины , наз. разбросом булевой функции . Здесь

где и - произвольные тупиковые д. н. ф., реализующие , а - число букв в тупиковой д. н. ф. Т. Построены примеры булевых функций, у к-рых ; установлено, однако, что для "почти всех" булевых функций

Приведенные выше оценки позволяют получить полное представление о тех трудностях, к-рые возникают при минимизации булевых функций по схеме: совершенная д. н. ф.- сокращенная д. н. ф.- тупиковая д. н. ф. - минимальная д. н. ф.

Лит.:[1] Васильев Ю. Л., "Проблемы кибернетики", 1963, в. 10, с. 5-61; [2] Глаголев В. В., "Проблемы кибернетики", 1967, в. 19, с. 75-94; [3] Коршунов А. Д., "Кибернетика", 1969, т. 6, с. 1-8; [4] Сапоженко А. А., "Матем. заметки", 1968, т. 4, № 6, с. 649-58. Ю. И. Журавлев.