ОСНАЩЕННОЕ ГИЛЬБЕРТОВО ПРОСТРАНСТВО

гильбертово пространство H с выделенным в нем линейным всюду плотным подмножеством , на к-ром задана структура топологического векторного пространства так, что вложение непрерывно. Это вложение порождает непрерывное вложение сопряженных пространств и цепочку непрерывных вложений (с помощью стандартного отождествления H'=H). Наиболее содержательным является случай, когда оснащение Ф - ядерное пространство. Здесь верно следующее усиление спектральной теоремы для самосопряженных операторов, действующих в Н:любой такой оператор А, непрерывно (в топологии Ф) переводящий Ф в себя, обладает полной системой обобщенных собственных функций {,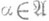} ( - нек-рое множество индексов), т. е. таких элементов , что для любого

причем множество значений функции 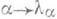, содержится в спектре оператора Аи имеет полную меру относительно спектральной меры , , , любого элемента . Полнота системы означает, что , для любого хотя бы при одном . Кроме того, для любого элемента существует его разложение по системе обобщенных собственных функций 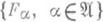, обобщающее известное разложение по базису собственных векторов для оператора с дискретным спектром.

П р и м е р: разложение в интеграл Фурье

- система обобщенных собственных функций оператора дифференцирования, действующего в , возникающая при естественном оснащении этого пространства с помощью пространства Шварца 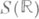. Аналогичные утверждения верны и для унитарных операторов, действующих в О. г. п.

Лит.:[1] Гельфанд И. М., Шилов Г. Е., Некоторые вопросы теории дифференциальных уравнений, М., 1958; [2] Гельфанд И. М., Виленкин Н. Я., Некоторые применения гармонического анализа. Оснащенные гильбертовы пространства, М., 15)61; [3] Березанский Ю. М., Разложение по собственным функциям самосопряженных операторов, К., 1965. Р. А. Минлос.