- МИНКОВСКОГО НЕРАВЕНСТВО
- 1) Собственно М. н.: если действительные числа
при i=l, . . ., n и р>1, то
Выведено Г. Минковским [1]. При
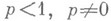неравенство заменяется на противоположное (для р<0 следует считать 
). В каждом из этих случаев равенство имеет место тогда и только тогда, когда строки 
и 
пропорциональны. При р=2 М. н. наз. неравенством треугольника. М. н. допускает обобщения в различных направлениях (они также носят названия неравенств Минковского ). Ниже приводятся нек-рые из них.2) М. н. для сумм. Пусть
для i=1, ... . . ., пи j = 1, . . ., ти р>1, тогда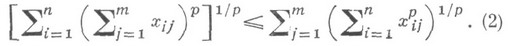
Знак неравенства меняется на обратный при р<1,
и для 
полагается 
. В каждом из этих случаев равенство имеет место тогда и только тогда, когда строки 
пропорциональны. Существуют также обобщения неравенств (1) на кратные и бесконечные суммы. Однако при использовании предельных процессов особого внимания требует формулировка случаев возможного равенства (см. [2]).Неравенства (1) и (2) однородны относительно
, и потому они имеют аналоги для различных средних, напр., если 
где 
то
подробнее см. в [2].
3) М. н. для интегралов аналогично неравенству (2) и имеет место опять же вследствие однородности относительно
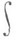. Пусть 
- интегрируемые функции в нек-рой области 
относительно элемента объема dV, тогда при р>1
Естественно получается обобщение неравенства (3) для большего числа функций. Дальнейшее обобщение: если k>1, то
причем равенство имеет место лишь в случае 
4) Другие неравенства типа М. н.:
а) для произведений: если
,то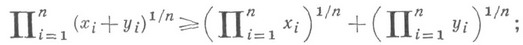
б) неравенство Малера: пусть F(x)- обобщенная норма в
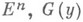- ее полярная функция. Тогда
где (Х, Х) - скалярное произведение;
в) для определителей: если А, В- неотрицательные эрмитовы матрицы над
, то
5) Наконец, с именем Г. Минковского связываются и др. неравенства, в особенности в выпуклом анализе и теории чисел, напр. Брунна- Минковского теорема.
Лит.:[1] Minkowski H., Geometrie uer Zahlen, 1, Lpz., 1896, § 115-17; [2] Xарди Г. Г., Литтльвуд Д ж., Полна Г., Неравенства, пер. с англ., М., 1948; [3] Беккен6ах Э. Ф., Беллман Р., Неравенства, пер. с англ., М., 1965; [4] Маркус М., Минк X., Обзор по теории матриц и матричных неравенств, пер. с англ., М., 1972.
М. И. Войцеховский.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
