МАТЕМАТИЧЕСКАЯ ЭКОНОМИКА

- математическая дисциплина, предметом к-рой являются модели экономич. объектов и процессов и методы их исследования. Однако понятия, результаты, методы М. э. удобно и принято излагать в тесной связи с их экономич. происхождением, интерпретацией и практич. приложениями. Особенно существенна связь с экономич. наукой и практикой.

М. э. как часть математики начала развиваться только в 20 в. Ранее были лишь эпизодпч. исследования, к-рые .нельзя в строгом смысле отнести к математике.

Особенности экономико-математического моделирования. Особенность экономич. моделирования состоит в исключительном разнообразии и разнородности предмета моделирования. В экономике присутствуют элементы управляемости и стихийности, жесткой определенности и существенной неоднозначности и свободы выбора, процессы технич. характера и социальные процессы, где на первый план выдвигается поведение человека. Разные уровни экономики (напр., цех и народное хозяйство) требуют существенно различного описания. Все это приводит к большой разнородности моделей математич. аппарата. Тонким вопросом является форма отражения типа социально-экономич. системы, к-рая моделируется, учет общественного строя. Нередко оказывается, что абстрактная математич. модель того или иного экономич. объекта или процесса с успехом применима и к капиталистической, и к социалистической экономике. Все дело в способе использования, интерпретации результатов анализа.

Производство, эффективное производство. Экономика имеет дело с благами, или продуктами, к-рые понимаются в М. э. чрезвычайно широко. Для них применяется общий термин ингредиенты. Ингредиентами являются услуги, природные ресурсы, отрицательно воздействующие на человека факторы окружающей среды, характеристика комфортности от имеющейся системы безопасности и т. д. Обычно считается, что число ингредиентов конечно и пространство продуктов есть - евклидово пространство, где l - число ингредиентов. Точка z из при надлежащих условиях может рассматриваться как "производственный" способ, положительные компоненты указывают объемы выпуска соответствующих ингредиентов, а отрицательные - затраты. Слово "производственный" взято в кавычки, поскольку производство понимается в самом широком смысле. Множество наличных (заданных, существующих) производственных возможностей есть Способ производства эффективен, если не существует такой, что и хотя бы для одной компоненты выполняется строгое неравенство. Задача выявления эффективных способов - одна из важнейших в экономике. Обычно предполагается, и это во многих случаях хорошо согласуется с действительностью, что Z - выпуклый компакт. С помощью расширения пространства продуктов задача анализа эффективных способов при этом может быть сведена к случаю, когда Z - выпуклый замкнутый конус.

Типичной задачей выявления эффективного способа является основная задача произведственного планирования. Задано множество производственных способов и вектор потребностей и ресурсных ограничений Требуется найти способ такой, что для всех 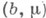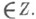Если Z - выпуклый замкнутый конус, то это есть общая задача выпуклого программирования. Если Zзадан конечным числом образующих (так наз. базисных способов), то это общая задача линейного программирования. Решение 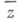лежит на границе Z. Пусть p - коэффициенты опорной гиперплоскости для Z в точке т. е. 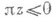для всех 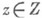и Основная теорема выпуклого программирования находит условия, при к-рых p_l>0. Напр., достаточно условия: существует вектор (так наз. условие Слейтера). Коэффициенты я, характеризующие эффективный способ имеют важный экономич. смысл. Они интерпретируются как цены, соизмеряющие эффективность затрат и выпуска отдельных ингредиентов. Способ эффективен тогда и только тогда, когда стоимость выпуска, равна стоимости затрат. Данная теория эффективных способов производства и их характеризации с помощью p оказала революционизирующее влияние на теорию и практику планирования социалистич. экономики. Она легла в основу объективных количественных методов определения цен и общественных оценок ресурсов, дающих возможность выбора наиболее эффективных экономич. решений в условиях социалистич. хозяйства. Теория естественным образом обобщается на бесконечное число ингредиентов. Тогда пространство ингредиентов оказывается подходящим образом выбранным функциональным пространством.

Эффективный рост. Ингредиенты, относящиеся к разным моментам или интервалам времени, формально можно считать различными. Поэтому описание производства в динамике в принципе укладывается в изложенную выше схему, состоящую из объектов {X, Z, b}, где X - пространство ингредиентов, Z - множество производственных возможностей, b - задания требований и ограничений на экономику. Однако изучение собственно динамич. аспекта производства требует более специальных форм описания производственных возможностей.

Производственные возможности достаточно общей модели экономич. динамики задаются с помощью точечно-множественного отображения (многозначной функции) Здесь - (фазовое) пространство экономики, интерпретируется как состояние экономики в тот или иной момент времени, где х _k - количество продукта k, имеющегося в наличии в этот момент. Множество а(х).состоит из всех состояний экономики, в к-рые она может перейти за единичный временной интервал из состояния х. Будем называть

графиком отображения а. Точки ( х, у).- допустимые производственные процессы.

Рассматриваются различные варианты задания возможных траекторий развития экономики. В частности, потребление населения учитывается либо в самом отображении я, либо выделяется в явном виде. Напр., во втором случае допустимой траекторией является последовательность такая, что

для всех t. Изучаются различные понятия эффективности траекторий. Траектория эффективна по потреблению, если не существует другой допустимой траектории (X, С), выходящей из того же начального состояния, для к-рой Траектория внутренне эффективна, если не существует другой допустимой траектории (X, С), выходящей из того же начального состояния, момента времени t₀ и числа l>1, что

Оптимальность траектории обычно определяется в зависимости от функции полезности и коэффициента приведения полезности во времени (о функции полезности см. ниже). Траектория наз. (и, m)-о птпмальной, если

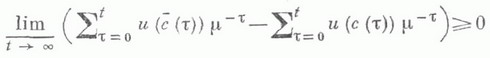
для любой допустимой траектории (X, С), выходящей из того же начального состояния. Имеется ряд довольно общих теорем существования для соответствующих траекторий.

Эффективные в различных смыслах траектории характеризуются последовательностью цен точно так же, как эффективный способ характеризовался ценами (коэффициентами опорной гиперплоскости) п. Т. е. если для эффективного способа стоимость затрат равна стоимости выпуска в оптимальных ценах, то на эффективной траектории стоимость состояний постоянна и максимальна, а на всех других допустимых траекториях не может возрастать.

Все приведенные определения легко обобщаются на случай, когда производственное отображение а, функция ии коэффициент m зависят от времени. Само время может быть непрерывным или вообще параметр tможет пробегать множество довольно произвольного вида.

С экономич. точки зрения интерес представляют траектории, на к-рых достигается максимально возможный темп роста экономики, к-рый она может выдержать сколь угодно долго. Оказывается, что при неизменных во времени а и и такие траектории являются стационарными, т. е. имеют вид

где а - темп роста (расширения) экономики. Стационарные эффективные в том или ином смысле, а также стационарные оптимальные траектории наз. магистралями.

При весьма широких предположениях имеют место теоремы о магистрали, утверждающие, что всякая эффективная траектория, независимо от начального состояния, с течением времени приближается к магистрали. Имеется большое число различных теорем о магистрали, различающихся определением эффективности или оптимальности, способом измерения расстояния до магистрали, типом сходимости, наконец, конечным или бесконечным временным интервалом.

Модель экономич. динамики, у к-рой производственные возможности задаются многогранным выпуклым конусом, наз. моделью Неймана. Частным случаем модели Неймана является замкнутая модель Леонтьева, или (по другой терминологии) замкнутый динамический межотраслевой баланс (термин "замкнутый" используется здесь как характеристика свойства экономики, состоящего в отсутствии невоспроизводимых продуктов), к-рый задается тремя матрицами с неотрицательными элементами Ф, Аи Впорядка Процесс тогда и только тогда, когда найдутся векторы v,такие, что выполнены неравенства:

Модель межотраслевого баланса получила большое распространение из-за удобства получения исходной информации для ее построения.

Модели экономич. динамики рассматриваются также в непрерывном времени. Одними из первых стали изучать как раз модели с непрерывным временем. В частности, ряд работ был посвящен простейшей однопродуктовой модели, задаваемой уравнением

где х - объем фондов, приходящихся на единицу трудовых ресурсов, с - потребление на душу населения, f- производственная функция (возрастающая, вогнутая). Неотрицательные функции удовлетворяющие этому уравнению, характеризуют допустимую траекторию. Для заданной функции полезности ии коэффициента дисконтирования mопределяется оптимальная траектория. Оптимальные траектории (и только они) удовлетворяют аналогу уравнения Эйлера

где - максимальное число, удовлетворяющее условию f(x) -с=х.

Модель Леонтьева также была сначала сформулирована в непрерывном времени в виде системы дифференциальных уравнений

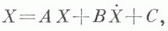
где X - потоки продуктов, Аи В - матрицы текущих и капитальных затрат соответственно, С - потоки конечного потребления.

Эффективные и оптимальные траектории в моделях с непрерывным временем изучаются с помощью методов вариационного исчисления, оптимального управления, математич. программирования в бесконечномерных пространствах. Рассматриваются также модели, допустимые траектории в к-рых задаются дифференциальными включениями вида (х), где а - производственное отображение.

Рациональное поведение потребителей. Вкусы и цели потребителей, к-рые определяют их рациональное поведение, даются в виде нек-рой системы предпочтений в пространстве продуктов. А именно, для каждого потребителя iопределено точечно-множественное отображение где Z - нек-рое пространство ситуаций, в к-рых может оказаться потребитель в процессе выбора, X - множество векторов, доступных потребителю, В частности, Zможет включать в себя в качестве подпространства Содержательно множество состоит из всех векторов к-рые (строго) предпочитаются вектору хв ситуации z. Напр., отображение Р _i может быть задано в виде функции полезности и, где и(х).показывает полезность от потребления набора продуктов х. Тогда

Пусть в описание ситуации z входят цены p. на все продукты и денежный доход потребителя d. Тогда 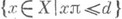есть множество наборов, к-рые потребитель может приобрести в ситуации z. Это множество наз. бюджетным. Рациональность поведения потребителя заключается в том, что он выбирает такие наборы хиз B_i(z), для к-рых Пусть D(z) - множество наборов продуктов, выбираемых истребителем г в ситуации z; D_i наз. отображен и-е м (или функцией в случае, когда D_i(z) состоит из одной точки) спроса. Имеется ряд исследований, посвященных выяснению свойств отображений Р _i, В _i, D_i. В частности, довольно подробно изучен случай, когда отображения Р _i могут быть заданы в виде функций. Определены условия, при к-рых отображения В _i и D_i являются непрерывными. Особый интерес представляет изучение свойств функции спроса D_i. Дело в том, что иногда удобнее считать в качестве первичных именно функции спроса D_i, а не предпочтения P_i, поскольку их легче построить по имеющейся информации о поведении потребителей. Напр., в экономике (торговая статистика) могут наблюдаться величины, приближенно оценивающие частные производные

где Яр - цена на продукт р, d - доход.

К теории рационального поведения потребителей примыкает теория группового выбора, имеющая дело, как правило, с дискретными вариантами. Обычно предполагается, что имеется конечное число участников группы и конечное число, напр., альтернативных вариантов. Задача состоит в выборе группового решения о выборе одного из вариантов при заданных отношениях предпочтения между вариантами для каждого участника. Групповой выбор обеспечивает различные схемы голосования, рассматриваются также аксиоматический и теоретико-игровой подходы.

Согласование интересов. Носителями интересов являются отдельные части экономич. системы, а также общество в целом. В качестве таких частей выступают потребители (группы потребителей): предприятия, министерства, территориальные органы управления, плановые и финансовые органы и т. п. Различают два взаимно переплетающихся подхода к проблеме согласования интересов - аналитический, или конструктивный, и синтетический, или дескриптивный. Согласно первому подходу в качестве исходного принимается глобальный критерий оптимальности (формализация интересов всего общества в целом). Задача состоит в том, чтобы вывести локальные (частные) критерии из общего, учитывая при этом частные интересы. При втором подходе исходными являются как раз частные интересы и задача заключается в объединении их в единую непротиворечивую систему, функционирование к-рой приводит к результатам, удовлетворительным с точки зрения всего общества в целом.

К первому подходу впрямую относятся декомпозиционные методы математич. программирования. Пусть, напр., в экономике имеется тпроизводителен и каждый производитель j задается множеством производственных возможностей Y_j, где и является выпуклым компактом. Задана целевая функция Vвсего общества в целом, где - вогнутая функция. Экономика должна быть организована таким образом, чтобы решалась задача выпуклого программирования: найти из условий

По теореме о характеристике эффективных способов производства существуют цены такие, что

для всех j,

Величина y^(j)pинтерпретируется как прибыль j-го производителя при ценах р. Отсюда следует, что критерий максимизации прибыли у каждого из производителей не противоречит общей цели, если действующие цены определены соответствующим образом. Схемы, относящиеся ко второму подходу, получили большое развитие в рамках моделей экономич. равновесия.

Экономическое равновесие. Предполагается, что экономика состоит из отдельных частей, являющихся носителями собственных интересов: производителей, занумерованных индексами j = 1, ..., т, и потребителей, занумерованных индексами i=1, ..., п. Производитель j описывается множеством производственных возможностей и отображением задающим его систему предпочтений. Здесь Z - множество возможных состояний экономики, конкретизируемое ниже. Потребитель г описывается множеством возможных наборов продуктов, доступных для потребления, начальным запасом продуктов предпочтением и, наконец, функцией распределения доходов, где a_i(z) показывает количество денег, поступающих потребителю i в состоянии z. Множество возможных цен в экономике есть Q. Тогда множество возможных состояний есть Бюджетное отображение B_i определяется здесь так:

Состояние равновесия описанной экономики есть удовлетворяющее условиям

По существу состояние равновесия экономики совпадает с определением решения бескоалиционной игры многих лиц в смысле Неймана - Нэша с дополнительным условием, чтобы выполнялся баланс по всем продуктам. Существование состояния равновесия доказано при весьма общих условиях для исходной экономики. Гораздо более жесткие условия необходимо накладывать для того, чтобы состояние равновесия было оптимальным, т. е. доставляло решение нек-рой глобальной оптимизационной задаче с целевой функцией, зависящей от интересов потребителей. Напр., пусть Р _i задано вогнутой непрерывной функцией a F_j задано функцией

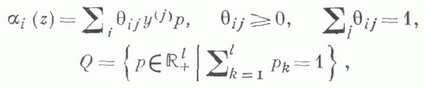
где Y_j, Х _i - выпуклые компакты,

Любое подмножество S={i₁, ..., i_r} индексов потребителей образует подэкономику исходной экономики, в к-рой каждому потребителю i_s из S соответствует (один и только один) производитель, множество производственных возможностей к-рого есть

Функции распределения доходов при этом имеют вид

Состояние наз. сбалансированным, если

Говорят, что сбалансированное состояние z исходной экономики блокируется коалицией потребителей S, если в подэкономике, определяемой коалицией S, существует такое сбалансированное состояние что для s=1, ..., r и хотя бы для одного индекса имеет место строгое неравенство. Ядром экономики наз. множество всех сбалансированных состояний, к-рые не блокируются никакой коалицией потребителей. Для экономики с описанными свойствами имеет место теорема: всякое состояние равновесия принадлежит ядру. Обратное неверно, однако найден ряд достаточных условий, при к-рых множество состояний равновесия и ядро близки друг к другу или вообще совпадают. В частности, если число потребителей стремится к бесконечности и влияние каждого потребителя на состояние экономики становится все более малым, то множество состояний равновесия стремится к ядру. Совпадение ядра и множества состояний равновесия имеет место в экономике с бесконечным (континуальным) числом потребителей (теорема Аумана).

Пусть экономика является моделью рынка (т. е. отсутствуют производители), множество участников (потребителей) к-рой является замкнутым единичным отрезком [0, 1], обозначаемым далее Т. Состояние экономики есть z=(x, p), где хесть функция, отображающая Тв R₊^l, каждая компонента к-рой интегрируема по Лебегу на отрезке Т. Начальное распределение продуктов между участниками задано функцией w,. таким образом сбалансированное состояние z таково, что 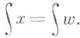Коалиция участников - это измеримое по Лебегу подмножество множества Т. Если подмножество имеет меру 0, то соответствующая коалиция наз. нулевой. Ядро - это множество всех сбалансированных состояний, к-рые не блокируются ни одной ненулевой коалицией. Состояние является равновесием, если для почти каждого участника i

Теорема Аумана утверждает, что в описанной экономике ядро и множество состояний равновесия совпадают. Интерес представляет вопрос о структуре множества состояний равновесия, в частности когда это множество конечно или состоит из одной точки. Здесь имеет место теорема Дебре. Пусть множество моделей рынка где суть начальные запасы продуктов у участника i, вектор является параметром, определяющим конкретную модель из множества Отображение представляет собой функцию спроса для i-гo участника. Функции D₁, ..., D_n заданы (не меняются) для всего множества экономик W. Пусть W₀, -совокупность экономик, у к-рых множество состояний равновесия бесконечно. Теорема Дебре утверждает, что если функции D₁, ... , D_n непрерывно дифференцируемы и отсутствуют точки насыщения хотя бы для одного из участников, то замыкание множества W₀ имеет (лебегову) меру нуль в пространстве W.

О численных методах. М. э. имеет тесную связь с вычислительной математикой. Линейное программирование, линейные экономич. модели оказали большое влияние на вычислительные методы линейной алгебры. По существу благодаря линейному программированию неравенства в вычислительной математике стали столь же употребительны, как и уравнения.

Трудным и многоплановым вопросом является вычисление экономич. равновесия. Напр., много работ посвящено условиям сходимости к равновесию системы дифференциальных уравнений

где р - вектор цен, F - функция избыточного спроса, т. е. разность функций спроса и предложения. Равновесные цены по определению, обеспечивают равенство спроса и предложения:

Функция избыточного спроса Fзадается либо непосредственно, либо через более первичные понятия соответствующей модели равновесия. С. Смейлом [8] изучена существенно более общая динамич. система, чем (*), применительно к модели рынка; наряду с изменением во времени цен р рассмотрено изменение состояния х;при этом допустимая траектория удовлетворяет нек-рым дифференциальным включениям вида где К(р).и С(р) - множества возможных направлений изменения ри х, определенные через модель рынка.

Экономич. равновесие, решение игры, решение той или иной экстремальной задачи могут быть определены как неподвижные точки подходящим образом сформулированного точечно-множественного отображения. В рамках исследований по М. э. разрабатываются численные методы поиска неподвижных точек разных классов отображений. Наиболее известен метод Скарфа, к-рый является комбинацией идей леммы Шпернера и симплекс-метода решения задач линейного программирования.

Смежные вопросы. М. э. тесно связана со многими математич. дисциплинами. Иногда трудно определить, где границы между М. э. и математич. статистикой или выпуклым анализом, функциональным анализом, топологией и т. д. Можно указать, напр., на развитие теории положительных матриц, положительных линейных (и однородных) операторов, спектральных свойств суперлинейных точечно-множественных отображений под влиянием потребностей М. э.

Лит.:[1]Нейман Дж., Моргенштерн О., Теория игр и экономическое поведение, пер. с англ., М., 1970; [2] К а н т о р о в и ч Л. В., Экономический расчет наилучшего использования ресурсов, М., 1959; [3] Никайдо X., Выпуклые структуры и математическая экономика, пер. с англ., М., 1972; [4] М а к а р о в В. Л., Рубинов А. М., Математическая теория экономической динамики и равновесия, М., 1973; [5] М и р к и н Б. Г., Проблема группового выбора [информации], М., 1974; [6] Scarf H., The Computation of Economic Equilibria, L., 1973; [7] Данциг Д ж., Линейное программирование, его применения и обобщения, пер. с англ., М., 1966; [8] Smale S., "J. math. Economics", 1976, №2, p. 107-20. Л. В. Канторович, В. Л. Макаров.