ЗНАЧИМОСТИ КРИТЕРИЙ

- один из основных методов статистич. проверки гипотез, применяемый для проверки соответствия результатов наблюдений х ₁,. .., х _п, трактуемых как реализации случайных величин Х ₁, ..., Х _п, нек-рой гипотезе Н ₀ о вероятностном распределении этих случайных величин. 3. к. отвергает либо принимает гипотезу Н ₀ в зависимости от наблюденного значения нек-рой статистики Т=Т (Х ₁,..., Х _п), конкретизация к-рой зависит от постановки задачи. При применении 3. к., вообще говоря, не предполагается наличие какой-либо конкурирующей гипотезы Н ₁, к-рую принимают в случае отклонения H₀, но если Ну задана, то, согласно общей теории статистич. проверки гипотез, именно конкурирующая гипотеза Н ₁ определяет выбор статистики Тв соответствии c принципом максимизации мощности критерия.

Обычно 3. к. применяют следующим образом. Выбрав статистику критерия Т( Х ₁, ..., Х _п), по ее распределению при гипотезе Н ₀ и по заранее выбранному уровню значимости а, 0<a<0,5, определяют критическое значение критерия t_a такое, что Согласно 3. к. с уровнем агипотезу Н _а отвергают, если Если Т( х ₁, . . ., x_n)<t_a, то считают, что гипотеза Н ₀ не противоречит результатам наблюдений х ₁,. . ., х _n, по крайней мере, до тех пор, пока новые результаты наблюдений не заставят экспериментатора принять другую точку зрения.

Пример. Если за первый час работы счетчик зарегистрировал 150 импульсов пуассоновского процесса, а за второй - 117 импульсов, то спрашивается, можно ли считать, что интенсивность поступления импульсов в единицу времени была постоянной (гипотеза Н ₀)?

Если гипотеза Н ₀ верна, то наблюденные значения 150 и 117 можно трактовать как реализации двух независимых случайных величин Х ₁ и Х ₂, подчиняющихся одному и тому же закону Пуассона с параметром Я, значение к-рого нам неизвестно. Поскольку при гипотезе Н ₀ случайные величины

приближенно подчиняются нормальному распределению с параметрами (0, 1), то статистика

распределена приближенно по закону c² с одной степенью свободы, т. е.

По таблицам c² -распределения находят критическое значение соответствующее заданному уровню значимости a=0,05, т. е.

Далее, по наблюденным значениям Х ₁=150 и Х ₂=117 вычисляют значение X² статистики критерия:

Поскольку 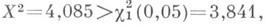то гипотеза Н ₀ о сохранении интенсивности отвергается по 3. к. типа х ² с уровнем значимости a=0,05.

Лит.:[1] Крамер Г., Математические методы статистики, пер. с англ., 2 изд., М., 1975; [2] Леман Э., Проверка статистических гипотез, пер. с англ., М., 1964; [3] Смирнов Н. В., Дунин-Барковский И. В., Курс теории вероятностей и математической статистики для технических приложений, 3 изд., М., 1969; [4] Девятов Б. И., "Теория вероятн. и ее примен.", 1969, т. 14, № 1, с. 175-78.

М. С. Никулин.