ДИКОЕ ВЛОЖЕНИЕ

топологического пространства Xв топологическое пространство Y- вложение, к-рое топологически не эквивалентно вложению из нек-рого класса выделенных вложений, наз. правильными, или ручными, вложениями. Наиболее употребительными являются следующие случаи; в качестве Yв них берется n-мерное евклидово пространство Rⁿ.

1) Пусть Месть k-мерное топологич. многообразие. Топологич. вложение g:наз. диким, если не существует гомеоморфизма Rⁿ на себя, переводящего g(M)в локально плоское подмногообразие Rⁿ.

2) Пусть Ресть k-мерный полиэдр. Топологич. вложение g:наз. диким, если не существует гомеоморфизма Rⁿ на себя, переводящего g(P)в полиэдр (т. е. в тело нек-рой триангуляции) Rⁿ.

3) Пусть Кесть k-мерное локально компактное пространство. Топологич. вложение g: наз. диким, если не существует гомеоморфизма Rⁿ на себя, переводящего g{K )в подмножество k-мерного Менгера компакта

Если размерность и то введенные свойства во всех трех случаях характеризуются локально гомотопич. свойством: вложение является диким тогда и только тогда, когда g(X)не удовлетворяет свойству 1-ULC (см. Топология вложений). Положение вещей для коразмерностей п-k=1. и 2 значительно сложнее: вопрос решен здесь для многообразий коразмерности 1 при 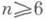и не решен полностью для вложений коразмерности 2 как для многообразий, так и для полиэдров. Все сказанное имеет смысл и тогда, когда в качестве Yберется n-мерное многообразие, топологическое или кусочно линейное. М. А. Штанько.