ДЕЛЕНИЯ КРУГА МНОГОЧЛЕН

круговой многочлен,- многочлен, имеющий вид

где j_k - первообразные корни степени n из единицы и произведение берется по всем числам к, взаимно простым с n и взятым из ряда 1, 2, . .., n. Степень многочлена Ф _п (х)- число натуральных чисел, меньших, чем л, и взаимно простых с га. Д. к. м. удовлетворяют соотношению где произведение берется по всем положительным делителям dчисла га, включая и само га. Это соотношение позволяет рекурсивно вычислять многочлены Ф _п (х)путем деления многочлена х ^п-1 на произведение всех Ф _d (х), d<n, d|n. При этом коэффициенты многочлена оказываются лежащими в исходном простом поле Р, а в случае поля рациональных чисел - целыми числами. Так,

Если п=р- простое и поле Римеет характеристику 0, то

Для многочлена Ф _п (х)можно указать явное выражение через Мёбиуса функциюm(k):

Напр.,

Над полем рациональных чисел все многочлены Ф _п (х)неприводимы, но над конечными простыми полями эти многочлены могут быть приводимы. Так, над полем вычетов по модулю 11 имеет место соотношение:

Уравнение Ф _n (х) = 0, дающее все первообразные корни п-й степени из единицы, наз. уравнением деления круга (окружности). Решение этого уравнения в тригонометрич. форме имеет вид:

где дробь kin несократима, т. е. ки пвзаимно просты. Решение в радикалах уравнения деления круга тесно связано с задачей построения правильного га-угольника или с эквивалентной ей задачей деления окружности на n равных частей, а именно, задача деления окружности на n частей решается с помощью циркуля и линейки тогда и только тогда, когда уравнение Ф _n(x) = 0 решается в квадратных радикалах. Последнее, как доказал К. Гаусс (С. Gauss, 1801), имеет место в том и только в том случае, когда

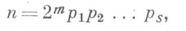
где т- целое неотрицательное число и р _1; р ₂,. .., p_s- попарно различные простые числа, представимые в виде 2^2k+1 с целым неотрицательным к.

Лит.:[1] Ван дер Варден Б. Л., Алгебра, пер. с нем., М., 1976; [2] Сушкевич А. К., Основы высшей алгебры, 4 изд., М.-Л., 1941.

П. В. Проскуряков.