ГРАДИЕНТНАЯ ДИНАМИЧЕСКАЯ СИСТЕМА

поток, задаваемый градиентом гладкой функции f на гладком многообразии. При дифференцировании f непосредственно получается ковариантный вектор (напр., в конечномерном случае в координатной окрестности Uс локальными координатами 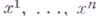это будет вектор с компонентами ), тогда как вектор фазовой скорости является контравариантным вектором. Переход от одного к другому осуществляется с помощью к.-л. римановой метрики, от выбора к-рой (наряду с f) зависит, таким образом, определение Г. д. с.; часто у вектора фазовой скорости еще меняют знак. В приведенном примере Г. д. с. в области Uописывается системой обыкновенных дифференциальных уравнений

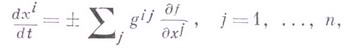
где коэффициенты образуют матрицу, обратную по отношению к матрице коэффициентов метрич. тензора; подразумевается, что во всех ге уравнениях правая часть берется с одним и тем же знаком "плюс" или "минус". Часто под Г. д. с. понимают системы несколько более общего типа (см. [1]).

Лит.:[1] S male S., "Ann. Math.", 1961, v. 74, p. 199-206.

Д. В. Аносов.