- ГИЛЬБЕРТОВА АЛГЕБРА
алгебра Ас инволюцией над полем комплексных чисел, снабженная невырожденным скалярным произведением (|), причем выполняются следующие аксиомы: 1)
для всех 
для всех 
3) для всех 
отображение 
пространства Ав Анепрерывно; 4) множество элементов вида 
, 
всюду плотно в А. Примерами гильбертовых алгебр являются алгебры 
(относительно свертки), где 
- компактная топологич. группа, и алгебра операторов Гильберта - Шмидта в данном гильбертовом пространстве.
Пусть А - Г. а., Н - гильбертово пространство - пополнение
- элементы алгебры ограниченных линейных операторов в H, являющиеся продолжениями по непрерывности умножений слева и справа на хв А. Отображение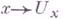 
(соответственно 
) есть невырожденное представление алгебры А(соответственно алгебры с инволюцией, противоположной А).в гильбертовом пространстве Н. Слабое замыкание семейства операторов 
(соответственно V).является алгеброй Неймана в Н;она наз. левой (соответственно правой) алгеброй Неймана данной Г. а. Аи обозначается 
(соответственно 
); 
и 
являются коммутантами друг друга; это - полуконечные алгебры Неймана. Любая Г. а. однозначно определяет нек-рый точный нормальный полуконечный след на алгебре Неймана 
; обратно, если дана алгебра Неймана 
и точный нормальный полуконечный след на 
, то можно построить Г. а. такую, что левая алгебра Неймана этой Г. а. изоморфна 
, и след, определяемый на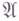 
Г. а., совпадает с исходным (см. [1]). Таким образом, Г. а. является средством изучения полуконечных алгебр Неймана и следов на них; нек-рое обобщение понятия Г. а. позволяет изучать аналогичными средствами не обязательно полуконечные алгебры Неймана (см. [2]). Лит.:[1] Dixmier J., Les algebres d'operateurs dans 1'espace hilbertien, 2 ed., P., 1969; [2] Тakesaki M., Tomita's theory of modular Hilbert algebras and its applications, В., 1970. А. И. Штерн.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
