ГЕОМЕТРИЧЕСКОЕ ПРИБЛИЖЕНИЕ
- ГЕОМЕТРИЧЕСКОЕ ПРИБЛИЖЕНИЕ
геометро-оптическое приближение, - ряд вида

к-рый формально удовлетворяет уравнению, описывающему волновой процесс (или системе уравнений, тогда  - векторы).
- векторы).
Для решения краевых задач теории колебаний (см. Дифракции математическая теория).разработан так наз. лучевой метод[2], позволяющий строить Г. п. Существует гипотеза, что получающиеся в результате ряды представляют собой асимптотич. разложение искомых решений там, где члены Г. п. не имеют особенностей. В частных случаях эту гипотезу удалось доказать. Имеется и нестационарный аналог Г. п.
Построение функций  основано на рассмотрении поля лучей, т. е. экстремалей функционала (см. Ферма принцип)
основано на рассмотрении поля лучей, т. е. экстремалей функционала (см. Ферма принцип)

где  - скорость в рассматриваемой изотропной физич. среде,
- скорость в рассматриваемой изотропной физич. среде,  - элемент длины дуги. Пусть пара параметров
- элемент длины дуги. Пусть пара параметров  характеризует луч, параметр
характеризует луч, параметр  - точки на луче, причем
- точки на луче, причем
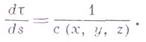
Параметры  можно взять за криволинейные координаты. Переход от криволинейных координат
можно взять за криволинейные координаты. Переход от криволинейных координат  ,
,  ,
,  к декартовой прямоугольной дается формулой
к декартовой прямоугольной дается формулой

Поверхности  ортогональны лучам. В тех точках, где поле лучей не имеет особенностей, отлична от нуля величина
ортогональны лучам. В тех точках, где поле лучей не имеет особенностей, отлична от нуля величина

к-рая наз. геометрическим расхождением. Величина J входит в рекуррентные соотношения, связывающие функции us между собой, и играет фундаментальную роль во всех построениях Г. п. Лит.:[1] Фридлендер Ф., 'Звуковые импульсы, пер. с англ., М., 1962; [2] Бабич В. М., Булдырев В. С., Асимптотические методы в задачах дифракции коротких волн, М., 1972. В. М. Бабич.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Полезное
Смотреть что такое "ГЕОМЕТРИЧЕСКОЕ ПРИБЛИЖЕНИЕ" в других словарях:
ЭЙКОНАЛА УРАВНЕНИЕ — уравнение с частными производными, имеющее вид Здесь т размерность пространства, с гладкая, не равная нулю функция. В приложениях симеет смысл скорости распространения волн, а поверхности волновых фронтов. Лучи (см. Ферма принцип )являются… … Математическая энциклопедия
Выпуклое тело — геометрическое тело, обладающее тем свойством, что соединяющий две его любые точки отрезок содержится в нём целиком. На рис. тело а выпукло, а тело б не выпукло. Шар, куб, шаровой сегмент, полупространство примеры В. т. Любая связная… … Большая советская энциклопедия
Задача Кеплера в общей теории относительности — Общая теория относительности … Википедия
Фондовый индекс — (Stock Code) Фондовый индекс это показатель изменения цен активов Фондовый индекс: определение, история, методы расчета, динамика, мировые и российские индексы, индекс Доу Джонса Содержание >>>>>>>>> … Энциклопедия инвестора
История арифметики — Арифметика. Роспись Пинтуриккьо. Апартаменты Борджиа. 1492 1495. Рим, Ватиканские дворцы … Википедия
Непрерывная дробь — Цепная дробь (или непрерывная дробь) это математическое выражение вида где a0 есть целое число и все остальные an натуральные числа (положительные целые). Любое вещественное число можно представить в виде цепной дроби (конечной или… … Википедия
Подходящая дробь — Цепная дробь (или непрерывная дробь) это математическое выражение вида где a0 есть целое число и все остальные an натуральные числа (то есть положительные целые). Любое вещественное число можно представить в виде цепной дроби (конечной или… … Википедия
Подходящие дроби — Цепная дробь (или непрерывная дробь) это математическое выражение вида где a0 есть целое число и все остальные an натуральные числа (то есть положительные целые). Любое вещественное число можно представить в виде цепной дроби (конечной или… … Википедия
Цепная дробь — (или непрерывная дробь) это математическое выражение вида где a0 есть целое число и все остальные an натуральные числа (то есть положительные целые). Любое вещественное число можно представить в виде цепной дроби (конечной или бесконечной). Число … Википедия
Метод хорд — Первые три итерации метода хорд. Синим нарисована функция f(x), красными проводятся хорды. Метод хорд итерационный численный метод приближённого нахождения … Википедия

 - векторы).
- векторы). основано на рассмотрении поля лучей, т. е. экстремалей функционала (см. Ферма принцип)
основано на рассмотрении поля лучей, т. е. экстремалей функционала (см. Ферма принцип)
 - скорость в рассматриваемой изотропной физич. среде,
- скорость в рассматриваемой изотропной физич. среде,  - элемент длины дуги. Пусть пара параметров
- элемент длины дуги. Пусть пара параметров  характеризует луч, параметр
характеризует луч, параметр  - точки на луче, причем
- точки на луче, причем 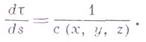
 можно взять за криволинейные координаты. Переход от криволинейных координат
можно взять за криволинейные координаты. Переход от криволинейных координат  ,
,  ,
,  к декартовой прямоугольной дается формулой
к декартовой прямоугольной дается формулой 
 ортогональны лучам. В тех точках, где поле лучей не имеет особенностей, отлична от нуля величина
ортогональны лучам. В тех точках, где поле лучей не имеет особенностей, отлична от нуля величина 
